树

字数统计: 4.4k字   |   阅读时长≈ 23分

递归

一棵树要么是空树，要么有两个指针，每个指针指向一棵树。树是一种递归结构，很多树的问题可以使用递归来处理。

1. 树的高度

104. Maximum Depth of Binary Tree (Easy)

Leetcode / 力扣

1
2
3
4
public int maxDepth(TreeNode root) {
    if (root == null) return 0;
    return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}

2. 平衡树

110. Balanced Binary Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

平衡树左右子树高度差都小于等于 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
private boolean result = true;

public boolean isBalanced(TreeNode root) {
    maxDepth(root);
    return result;
}

public int maxDepth(TreeNode root) {
    if (root == null) return 0;
    int l = maxDepth(root.left);
    int r = maxDepth(root.right);
    if (Math.abs(l - r) > 1) result = false;
    return 1 + Math.max(l, r);
}

3. 两节点的最长路径

543. Diameter of Binary Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
Input:

         1
        / \
       2  3
      / \
     4   5

Return 3, which is the length of the path [4,2,1,3] or [5,2,1,3].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
private int max = 0;

public int diameterOfBinaryTree(TreeNode root) {
    depth(root);
    return max;
}

private int depth(TreeNode root) {
    if (root == null) return 0;
    int leftDepth = depth(root.left);
    int rightDepth = depth(root.right);
    max = Math.max(max, leftDepth + rightDepth);
    return Math.max(leftDepth, rightDepth) + 1;
}

4. 翻转树

226. Invert Binary Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
public TreeNode invertTree(TreeNode root) {
    if (root == null) return null;
    TreeNode left = root.left;  // 后面的操作会改变 left 指针，因此先保存下来
    root.left = invertTree(root.right);
    root.right = invertTree(left);
    return root;
}

5. 归并两棵树

617. Merge Two Binary Trees (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Input:
       Tree 1                     Tree 2
          1                         2
         / \                       / \
        3   2                     1   3
       /                           \   \
      5                             4   7

Output:
         3
        / \
       4   5
      / \   \
     5   4   7
1
2
3
4
5
6
7
8
9
public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
    if (t1 == null && t2 == null) return null;
    if (t1 == null) return t2;
    if (t2 == null) return t1;
    TreeNode root = new TreeNode(t1.val + t2.val);
    root.left = mergeTrees(t1.left, t2.left);
    root.right = mergeTrees(t1.right, t2.right);
    return root;
}

6. 判断路径和是否等于一个数

Leetcdoe : 112. Path Sum (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
Given the below binary tree and sum = 22,

              5
             / \
            4   8
           /   / \
          11  13  4
         /  \      \
        7    2      1

return true, as there exist a root-to-leaf path 5->4->11->2 which sum is 22.

路径和定义为从 root 到 leaf 的所有节点的和。

1
2
3
4
5
public boolean hasPathSum(TreeNode root, int sum) {
    if (root == null) return false;
    if (root.left == null && root.right == null && root.val == sum) return true;
    return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
}

7. 统计路径和等于一个数的路径数量

437. Path Sum III (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8

      10
     /  \
    5   -3
   / \    \
  3   2   11
 / \   \
3  -2   1

Return 3. The paths that sum to 8 are:

1.  5 -> 3
2.  5 -> 2 -> 1
3. -3 -> 11

路径不一定以 root 开头，也不一定以 leaf 结尾，但是必须连续。

1
2
3
4
5
6
7
8
9
10
11
12
13
public int pathSum(TreeNode root, int sum) {
    if (root == null) return 0;
    int ret = pathSumStartWithRoot(root, sum) + pathSum(root.left, sum) + pathSum(root.right, sum);
    return ret;
}

private int pathSumStartWithRoot(TreeNode root, int sum) {
    if (root == null) return 0;
    int ret = 0;
    if (root.val == sum) ret++;
    ret += pathSumStartWithRoot(root.left, sum - root.val) + pathSumStartWithRoot(root.right, sum - root.val);
    return ret;
}

8. 子树

572. Subtree of Another Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Given tree s:
     3
    / \
   4   5
  / \
 1   2

Given tree t:
   4
  / \
 1   2

Return true, because t has the same structure and node values with a subtree of s.

Given tree s:

     3
    / \
   4   5
  / \
 1   2
    /
   0

Given tree t:
   4
  / \
 1   2

Return false.
1
2
3
4
5
6
7
8
9
10
11
public boolean isSubtree(TreeNode s, TreeNode t) {
    if (s == null) return false;
    return isSubtreeWithRoot(s, t) || isSubtree(s.left, t) || isSubtree(s.right, t);
}

private boolean isSubtreeWithRoot(TreeNode s, TreeNode t) {
    if (t == null && s == null) return true;
    if (t == null || s == null) return false;
    if (t.val != s.val) return false;
    return isSubtreeWithRoot(s.left, t.left) && isSubtreeWithRoot(s.right, t.right);
}

9. 树的对称

101. Symmetric Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
    1
   / \
  2   2
 / \ / \
3  4 4  3
1
2
3
4
5
6
7
8
9
10
11
public boolean isSymmetric(TreeNode root) {
    if (root == null) return true;
    return isSymmetric(root.left, root.right);
}

private boolean isSymmetric(TreeNode t1, TreeNode t2) {
    if (t1 == null && t2 == null) return true;
    if (t1 == null || t2 == null) return false;
    if (t1.val != t2.val) return false;
    return isSymmetric(t1.left, t2.right) && isSymmetric(t1.right, t2.left);
}

10. 最小路径

111. Minimum Depth of Binary Tree (Easy)

Leetcode / 力扣

树的根节点到叶子节点的最小路径长度

1
2
3
4
5
6
7
public int minDepth(TreeNode root) {
    if (root == null) return 0;
    int left = minDepth(root.left);
    int right = minDepth(root.right);
    if (left == 0 || right == 0) return left + right + 1;
    return Math.min(left, right) + 1;
}

11. 统计左叶子节点的和

404. Sum of Left Leaves (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
    3
   / \
  9  20
    /  \
   15   7

There are two left leaves in the binary tree, with values 9 and 15 respectively. Return 24.
1
2
3
4
5
6
7
8
9
10
public int sumOfLeftLeaves(TreeNode root) {
    if (root == null) return 0;
    if (isLeaf(root.left)) return root.left.val + sumOfLeftLeaves(root.right);
    return sumOfLeftLeaves(root.left) + sumOfLeftLeaves(root.right);
}

private boolean isLeaf(TreeNode node){
    if (node == null) return false;
    return node.left == null && node.right == null;
}

12. 相同节点值的最大路径长度

687. Longest Univalue Path (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
             1
            / \
           4   5
          / \   \
         4   4   5

Output : 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
private int path = 0;

public int longestUnivaluePath(TreeNode root) {
    dfs(root);
    return path;
}

private int dfs(TreeNode root){
    if (root == null) return 0;
    int left = dfs(root.left);
    int right = dfs(root.right);
    int leftPath = root.left != null && root.left.val == root.val ? left + 1 : 0;
    int rightPath = root.right != null && root.right.val == root.val ? right + 1 : 0;
    path = Math.max(path, leftPath + rightPath);
    return Math.max(leftPath, rightPath);
}

13. 间隔遍历

337. House Robber III (Medium)

Leetcode / 力扣

1
2
3
4
5
6
     3
    / \
   2   3
    \   \
     3   1
Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.
1
2
3
4
5
6
7
8
9
10
11
12
13
Map<TreeNode, Integer> cache = new HashMap<>(); 

public int rob(TreeNode root) {
    if (root == null) return 0;
    if (cache.containsKey(root)) return cache.get(root);
    int val1 = root.val;
    if (root.left != null) val1 += rob(root.left.left) + rob(root.left.right);
    if (root.right != null) val1 += rob(root.right.left) + rob(root.right.right);
    int val2 = rob(root.left) + rob(root.right);
    int res = Math.max(val1, val2);
    cache.put(root, res);
    return res;
}

14. 找出二叉树中第二小的节点

671. Second Minimum Node In a Binary Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
Input:
   2
  / \
 2   5
    / \
    5  7

Output: 5

一个节点要么具有 0 个或 2 个子节点，如果有子节点，那么根节点是最小的节点。

1
2
3
4
5
6
7
8
9
10
11
public int findSecondMinimumValue(TreeNode root) {
    if (root == null) return -1;
    if (root.left == null && root.right == null) return -1;
    int leftVal = root.left.val;
    int rightVal = root.right.val;
    if (leftVal == root.val) leftVal = findSecondMinimumValue(root.left);
    if (rightVal == root.val) rightVal = findSecondMinimumValue(root.right);
    if (leftVal != -1 && rightVal != -1) return Math.min(leftVal, rightVal);
    if (leftVal != -1) return leftVal;
    return rightVal;
}

层次遍历

使用 BFS 进行层次遍历。不需要使用两个队列来分别存储当前层的节点和下一层的节点，因为在开始遍历一层的节点时，当前队列中的节点数就是当前层的节点数，只要控制遍历这么多节点数，就能保证这次遍历的都是当前层的节点。

1. 一棵树每层节点的平均数

637. Average of Levels in Binary Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public List<Double> averageOfLevels(TreeNode root) {
    List<Double> ret = new ArrayList<>();
    if (root == null) return ret;
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    while (!queue.isEmpty()) {
        int cnt = queue.size();
        double sum = 0;
        for (int i = 0; i < cnt; i++) {
            TreeNode node = queue.poll();
            sum += node.val;
            if (node.left != null) queue.add(node.left);
            if (node.right != null) queue.add(node.right);
        }
        ret.add(sum / cnt);
    }
    return ret;
}

2. 得到左下角的节点

513. Find Bottom Left Tree Value (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
Input:

        1
       / \
      2   3
     /   / \
    4   5   6
       /
      7

Output:
7
1
2
3
4
5
6
7
8
9
10
public int findBottomLeftValue(TreeNode root) {
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    while (!queue.isEmpty()) {
        root = queue.poll();
        if (root.right != null) queue.add(root.right);
        if (root.left != null) queue.add(root.left);
    }
    return root.val;
}

前中后序遍历

1
2
3
4
5
    1
   / \
  2   3
 / \   \
4   5   6
  • 层次遍历顺序：[1 2 3 4 5 6]
  • 前序遍历顺序：[1 2 4 5 3 6]
  • 中序遍历顺序：[4 2 5 1 3 6]
  • 后序遍历顺序：[4 5 2 6 3 1]

层次遍历使用 BFS 实现，利用的就是 BFS 一层一层遍历的特性；而前序、中序、后序遍历利用了 DFS 实现。

前序、中序、后序遍只是在对节点访问的顺序有一点不同，其它都相同。

① 前序

1
2
3
4
5
void dfs(TreeNode root) {
    visit(root);
    dfs(root.left);
    dfs(root.right);
}

② 中序

1
2
3
4
5
void dfs(TreeNode root) {
    dfs(root.left);
    visit(root);
    dfs(root.right);
}

③ 后序

1
2
3
4
5
void dfs(TreeNode root) {
    dfs(root.left);
    dfs(root.right);
    visit(root);
}

1. 非递归实现二叉树的前序遍历

144. Binary Tree Preorder Traversal (Medium)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
13
public List<Integer> preorderTraversal(TreeNode root) {
    List<Integer> ret = new ArrayList<>();
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        TreeNode node = stack.pop();
        if (node == null) continue;
        ret.add(node.val);
        stack.push(node.right);  // 先右后左，保证左子树先遍历
        stack.push(node.left);
    }
    return ret;
}

2. 非递归实现二叉树的后序遍历

145. Binary Tree Postorder Traversal (Medium)

Leetcode / 力扣

前序遍历为 root -> left -> right，后序遍历为 left -> right -> root。可以修改前序遍历成为 root -> right -> left，那么这个顺序就和后序遍历正好相反。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public List<Integer> postorderTraversal(TreeNode root) {
    List<Integer> ret = new ArrayList<>();
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        TreeNode node = stack.pop();
        if (node == null) continue;
        ret.add(node.val);
        stack.push(node.left);
        stack.push(node.right);
    }
    Collections.reverse(ret);
    return ret;
}

3. 非递归实现二叉树的中序遍历

94. Binary Tree Inorder Traversal (Medium)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer> ret = new ArrayList<>();
    if (root == null) return ret;
    Stack<TreeNode> stack = new Stack<>();
    TreeNode cur = root;
    while (cur != null || !stack.isEmpty()) {
        while (cur != null) {
            stack.push(cur);
            cur = cur.left;
        }
        TreeNode node = stack.pop();
        ret.add(node.val);
        cur = node.right;
    }
    return ret;
}

BST

二叉查找树（BST）：根节点大于等于左子树所有节点，小于等于右子树所有节点。

二叉查找树中序遍历有序。

1. 修剪二叉查找树

669. Trim a Binary Search Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Input:

    3
   / \
  0   4
   \
    2
   /
  1

  L = 1
  R = 3

Output:

      3
     /
   2
  /
 1

题目描述：只保留值在 L ~ R 之间的节点

1
2
3
4
5
6
7
8
public TreeNode trimBST(TreeNode root, int L, int R) {
    if (root == null) return null;
    if (root.val > R) return trimBST(root.left, L, R);
    if (root.val < L) return trimBST(root.right, L, R);
    root.left = trimBST(root.left, L, R);
    root.right = trimBST(root.right, L, R);
    return root;
}

2. 寻找二叉查找树的第 k 个元素

230. Kth Smallest Element in a BST (Medium)

Leetcode / 力扣

中序遍历解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
private int cnt = 0;
private int val;

public int kthSmallest(TreeNode root, int k) {
    inOrder(root, k);
    return val;
}

private void inOrder(TreeNode node, int k) {
    if (node == null) return;
    inOrder(node.left, k);
    cnt++;
    if (cnt == k) {
        val = node.val;
        return;
    }
    inOrder(node.right, k);
}

递归解法：

1
2
3
4
5
6
7
8
9
10
11
public int kthSmallest(TreeNode root, int k) {
    int leftCnt = count(root.left);
    if (leftCnt == k - 1) return root.val;
    if (leftCnt > k - 1) return kthSmallest(root.left, k);
    return kthSmallest(root.right, k - leftCnt - 1);
}

private int count(TreeNode node) {
    if (node == null) return 0;
    return 1 + count(node.left) + count(node.right);
}

3. 把二叉查找树每个节点的值都加上比它大的节点的值

Convert BST to Greater Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
Input: The root of a Binary Search Tree like this:

              5
            /   \
           2     13

Output: The root of a Greater Tree like this:

             18
            /   \
          20     13

先遍历右子树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
private int sum = 0;

public TreeNode convertBST(TreeNode root) {
    traver(root);
    return root;
}

private void traver(TreeNode node) {
    if (node == null) return;
    traver(node.right);
    sum += node.val;
    node.val = sum;
    traver(node.left);
}

4. 二叉查找树的最近公共祖先

235. Lowest Common Ancestor of a Binary Search Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
        _______6______
      /                \
  ___2__             ___8__
 /      \           /      \
0        4         7        9
        /  \
       3   5

For example, the lowest common ancestor (LCA) of nodes 2 and 8 is 6. Another example is LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
1
2
3
4
5
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if (root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q);
    if (root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q);
    return root;
}

5. 二叉树的最近公共祖先

236. Lowest Common Ancestor of a Binary Tree (Medium)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
       _______3______
      /              \
  ___5__           ___1__
 /      \         /      \
6        2       0        8
        /  \
       7    4

For example, the lowest common ancestor (LCA) of nodes 5 and 1 is 3. Another example is LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
1
2
3
4
5
6
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if (root == null || root == p || root == q) return root;
    TreeNode left = lowestCommonAncestor(root.left, p, q);
    TreeNode right = lowestCommonAncestor(root.right, p, q);
    return left == null ? right : right == null ? left : root;
}

6. 从有序数组中构造二叉查找树

108. Convert Sorted Array to Binary Search Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
public TreeNode sortedArrayToBST(int[] nums) {
    return toBST(nums, 0, nums.length - 1);
}

private TreeNode toBST(int[] nums, int sIdx, int eIdx){
    if (sIdx > eIdx) return null;
    int mIdx = (sIdx + eIdx) / 2;
    TreeNode root = new TreeNode(nums[mIdx]);
    root.left =  toBST(nums, sIdx, mIdx - 1);
    root.right = toBST(nums, mIdx + 1, eIdx);
    return root;
}

7. 根据有序链表构造平衡的二叉查找树

109. Convert Sorted List to Binary Search Tree (Medium)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
Given the sorted linked list: [-10,-3,0,5,9],

One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

      0
     / \
   -3   9
   /   /
 -10  5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public TreeNode sortedListToBST(ListNode head) {
    if (head == null) return null;
    if (head.next == null) return new TreeNode(head.val);
    ListNode preMid = preMid(head);
    ListNode mid = preMid.next;
    preMid.next = null;  // 断开链表
    TreeNode t = new TreeNode(mid.val);
    t.left = sortedListToBST(head);
    t.right = sortedListToBST(mid.next);
    return t;
}

private ListNode preMid(ListNode head) {
    ListNode slow = head, fast = head.next;
    ListNode pre = head;
    while (fast != null && fast.next != null) {
        pre = slow;
        slow = slow.next;
        fast = fast.next.next;
    }
    return pre;
}

8. 在二叉查找树中寻找两个节点，使它们的和为一个给定值

653. Two Sum IV - Input is a BST (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
Input:

    5
   / \
  3   6
 / \   \
2   4   7

Target = 9

Output: True

使用中序遍历得到有序数组之后，再利用双指针对数组进行查找。

应该注意到，这一题不能用分别在左右子树两部分来处理这种思想，因为两个待求的节点可能分别在左右子树中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public boolean findTarget(TreeNode root, int k) {
    List<Integer> nums = new ArrayList<>();
    inOrder(root, nums);
    int i = 0, j = nums.size() - 1;
    while (i < j) {
        int sum = nums.get(i) + nums.get(j);
        if (sum == k) return true;
        if (sum < k) i++;
        else j--;
    }
    return false;
}

private void inOrder(TreeNode root, List<Integer> nums) {
    if (root == null) return;
    inOrder(root.left, nums);
    nums.add(root.val);
    inOrder(root.right, nums);
}

9. 在二叉查找树中查找两个节点之差的最小绝对值

530. Minimum Absolute Difference in BST (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
Input:

   1
    \
     3
    /
   2

Output:

1

利用二叉查找树的中序遍历为有序的性质，计算中序遍历中临近的两个节点之差的绝对值，取最小值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
private int minDiff = Integer.MAX_VALUE;
private TreeNode preNode = null;

public int getMinimumDifference(TreeNode root) {
    inOrder(root);
    return minDiff;
}

private void inOrder(TreeNode node) {
    if (node == null) return;
    inOrder(node.left);
    if (preNode != null) minDiff = Math.min(minDiff, node.val - preNode.val);
    preNode = node;
    inOrder(node.right);
}

10. 寻找二叉查找树中出现次数最多的值

501. Find Mode in Binary Search Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
   1
    \
     2
    /
   2

return [2].

答案可能不止一个，也就是有多个值出现的次数一样多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
private int curCnt = 1;
private int maxCnt = 1;
private TreeNode preNode = null;

public int[] findMode(TreeNode root) {
    List<Integer> maxCntNums = new ArrayList<>();
    inOrder(root, maxCntNums);
    int[] ret = new int[maxCntNums.size()];
    int idx = 0;
    for (int num : maxCntNums) {
        ret[idx++] = num;
    }
    return ret;
}

private void inOrder(TreeNode node, List<Integer> nums) {
    if (node == null) return;
    inOrder(node.left, nums);
    if (preNode != null) {
        if (preNode.val == node.val) curCnt++;
        else curCnt = 1;
    }
    if (curCnt > maxCnt) {
        maxCnt = curCnt;
        nums.clear();
        nums.add(node.val);
    } else if (curCnt == maxCnt) {
        nums.add(node.val);
    }
    preNode = node;
    inOrder(node.right, nums);
}

Trie


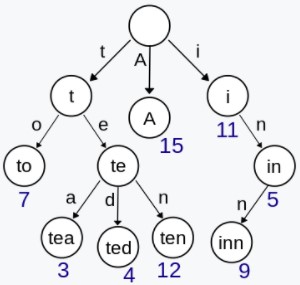
Trie，又称前缀树或字典树，用于判断字符串是否存在或者是否具有某种字符串前缀。

1. 实现一个 Trie

208. Implement Trie (Prefix Tree) (Medium)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Trie {

    private class Node {
        Node[] childs = new Node[26];
        boolean isLeaf;
    }

    private Node root = new Node();

    public Trie() {
    }

    public void insert(String word) {
        insert(word, root);
    }

    private void insert(String word, Node node) {
        if (node == null) return;
        if (word.length() == 0) {
            node.isLeaf = true;
            return;
        }
        int index = indexForChar(word.charAt(0));
        if (node.childs[index] == null) {
            node.childs[index] = new Node();
        }
        insert(word.substring(1), node.childs[index]);
    }

    public boolean search(String word) {
        return search(word, root);
    }

    private boolean search(String word, Node node) {
        if (node == null) return false;
        if (word.length() == 0) return node.isLeaf;
        int index = indexForChar(word.charAt(0));
        return search(word.substring(1), node.childs[index]);
    }

    public boolean startsWith(String prefix) {
        return startWith(prefix, root);
    }

    private boolean startWith(String prefix, Node node) {
        if (node == null) return false;
        if (prefix.length() == 0) return true;
        int index = indexForChar(prefix.charAt(0));
        return startWith(prefix.substring(1), node.childs[index]);
    }

    private int indexForChar(char c) {
        return c - 'a';
    }
}

2. 实现一个 Trie，用来求前缀和

677. Map Sum Pairs (Medium)

Leetcode / 力扣

1
2
3
4
Input: insert("apple", 3), Output: Null
Input: sum("ap"), Output: 3
Input: insert("app", 2), Output: Null
Input: sum("ap"), Output: 5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class MapSum {

    private class Node {
        Node[] child = new Node[26];
        int value;
    }

    private Node root = new Node();

    public MapSum() {

    }

    public void insert(String key, int val) {
        insert(key, root, val);
    }

    private void insert(String key, Node node, int val) {
        if (node == null) return;
        if (key.length() == 0) {
            node.value = val;
            return;
        }
        int index = indexForChar(key.charAt(0));
        if (node.child[index] == null) {
            node.child[index] = new Node();
        }
        insert(key.substring(1), node.child[index], val);
    }

    public int sum(String prefix) {
        return sum(prefix, root);
    }

    private int sum(String prefix, Node node) {
        if (node == null) return 0;
        if (prefix.length() != 0) {
            int index = indexForChar(prefix.charAt(0));
            return sum(prefix.substring(1), node.child[index]);
        }
        int sum = node.value;
        for (Node child : node.child) {
            sum += sum(prefix, child);
        }
        return sum;
    }

    private int indexForChar(char c) {
        return c - 'a';
    }
}

扫一扫，分享到微信

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia-plus根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

LHS

面朝大海
春暖花开