在线性回归中我们有一个像这样的训练集，𝑚代表了训练样本的数量，比如 𝑚 = 47。而我们的假设函数，也就是用来进行预测的函数，是这样的线性函数形式： ℎ𝜃(𝑥) = 𝜃0 + 𝜃1𝑥。我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度，模型所预测的值与训练集中实际值之间的差距（下图中蓝线所指）就是建模误差（modeling error）。

我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。 即使得代价函数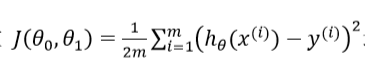达到最小。

我们绘制一个等高线图，三个坐标分别为𝜃0和𝜃1 和𝐽(𝜃0,𝜃1)，如下图所示，可以看出在三维空间中存在一个使得𝐽(𝜃0,𝜃1)最小的点。

为什么误差平方代价函数？代价函数也被称作平方误差函数，有时也被称为平方误差代价函数。我们之所以要求出误差的平方和，是因为误差平方代价函数，对于大多数问题，特别是回归问题，都是一个合理的选择。还有其他的代价函数也能很好地发挥作用，但是平方误差代价函数可能是解决回归问题最常用的手段了。