Spring boot笔记

一、Spring Boot 入门

1、Spring Boot 简介

简化Spring应用开发的一个框架；

整个Spring技术栈的一个大整合；

J2EE开发的一站式解决方案；

2、微服务

2014，martin fowler

微服务：架构风格（服务微化）

一个应用应该是一组小型服务；可以通过HTTP的方式进行互通；

单体应用：ALL IN ONE

微服务：每一个功能元素最终都是一个可独立替换和独立升级的软件单元；

详细参照微服务文档

more >>
置顶

展开全文 >>

排序

快速选择

用于求解 Kth Element 问题，也就是第 K 个元素的问题。

可以使用快速排序的 partition() 进行实现。需要先打乱数组，否则最坏情况下时间复杂度为 O(N2)。

堆

用于求解 TopK Elements 问题，也就是 K 个最小元素的问题。使用最小堆来实现 TopK 问题，最小堆使用大顶堆来实现，大顶堆的堆顶元素为当前堆的最大元素。实现过程：不断地往大顶堆中插入新元素，当堆中元素的数量大于 k 时，移除堆顶元素，也就是当前堆中最大的元素，剩下的元素都为当前添加过的元素中最小的 K 个元素。插入和移除堆顶元素的时间复杂度都为 log2N。

堆也可以用于求解 Kth Element 问题，得到了大小为 K 的最小堆之后，因为使用了大顶堆来实现，因此堆顶元素就是第 K 大的元素。

快速选择也可以求解 TopK Elements 问题，因为找到 Kth Element 之后，再遍历一次数组，所有小于等于 Kth Element 的元素都是 TopK Elements。

可以看到，快速选择和堆排序都可以求解 Kth Element 和 TopK Elements 问题。

1. Kth Element

215. Kth Largest Element in an Array (Medium)

Leetcode / 力扣

1
2
Input: [3,2,1,5,6,4] and k = 2
Output: 5

题目描述：找到倒数第 k 个的元素。

排序 ：时间复杂度 O(NlogN)，空间复杂度 O(1)

1
2
3
4
public int findKthLargest(int[] nums, int k) {
    Arrays.sort(nums);
    return nums[nums.length - k];
}

堆 ：时间复杂度 O(NlogK)，空间复杂度 O(K)。

1
2
3
4
5
6
7
8
9
public int findKthLargest(int[] nums, int k) {
    PriorityQueue<Integer> pq = new PriorityQueue<>(); // 小顶堆
    for (int val : nums) {
        pq.add(val);
        if (pq.size() > k)  // 维护堆的大小为 K
            pq.poll();
    }
    return pq.peek();
}

快速选择 ：时间复杂度 O(N)，空间复杂度 O(1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public int findKthLargest(int[] nums, int k) {
    k = nums.length - k;
    int l = 0, h = nums.length - 1;
    while (l < h) {
        int j = partition(nums, l, h);
        if (j == k) {
            break;
        } else if (j < k) {
            l = j + 1;
        } else {
            h = j - 1;
        }
    }
    return nums[k];
}

private int partition(int[] a, int l, int h) {
    int i = l, j = h + 1;
    while (true) {
        while (a[++i] < a[l] && i < h) ;
        while (a[--j] > a[l] && j > l) ;
        if (i >= j) {
            break;
        }
        swap(a, i, j);
    }
    swap(a, l, j);
    return j;
}

private void swap(int[] a, int i, int j) {
    int t = a[i];
    a[i] = a[j];
    a[j] = t;
}

桶排序

1. 出现频率最多的 k 个元素

347. Top K Frequent Elements (Medium)

Leetcode / 力扣

1
Given [1,1,1,2,2,3] and k = 2, return [1,2].

设置若干个桶，每个桶存储出现频率相同的数。桶的下标表示数出现的频率，即第 i 个桶中存储的数出现的频率为 i。

把数都放到桶之后，从后向前遍历桶，最先得到的 k 个数就是出现频率最多的的 k 个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public int[] topKFrequent(int[] nums, int k) {
    Map<Integer, Integer> frequencyForNum = new HashMap<>();
    for (int num : nums) {
        frequencyForNum.put(num, frequencyForNum.getOrDefault(num, 0) + 1);
    }
    List<Integer>[] buckets = new ArrayList[nums.length + 1];
    for (int key : frequencyForNum.keySet()) {
        int frequency = frequencyForNum.get(key);
        if (buckets[frequency] == null) {
            buckets[frequency] = new ArrayList<>();
        }
        buckets[frequency].add(key);
    }
    List<Integer> topK = new ArrayList<>();
    for (int i = buckets.length - 1; i >= 0 && topK.size() < k; i--) {
        if (buckets[i] == null) {
            continue;
        }
        if (buckets[i].size() <= (k - topK.size())) {
            topK.addAll(buckets[i]);
        } else {
            topK.addAll(buckets[i].subList(0, k - topK.size()));
        }
    }
    int[] res = new int[k];
    for (int i = 0; i < k; i++) {
        res[i] = topK.get(i);
    }
    return res;
}

2. 按照字符出现次数对字符串排序

451. Sort Characters By Frequency (Medium)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
Input:
"tree"

Output:
"eert"

Explanation:
'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr" is also a valid answer.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public String frequencySort(String s) {
    Map<Character, Integer> frequencyForNum = new HashMap<>();
    for (char c : s.toCharArray())
        frequencyForNum.put(c, frequencyForNum.getOrDefault(c, 0) + 1);

    List<Character>[] frequencyBucket = new ArrayList[s.length() + 1];
    for (char c : frequencyForNum.keySet()) {
        int f = frequencyForNum.get(c);
        if (frequencyBucket[f] == null) {
            frequencyBucket[f] = new ArrayList<>();
        }
        frequencyBucket[f].add(c);
    }
    StringBuilder str = new StringBuilder();
    for (int i = frequencyBucket.length - 1; i >= 0; i--) {
        if (frequencyBucket[i] == null) {
            continue;
        }
        for (char c : frequencyBucket[i]) {
            for (int j = 0; j < i; j++) {
                str.append(c);
            }
        }
    }
    return str.toString();
}

荷兰国旗问题

荷兰国旗包含三种颜色：红、白、蓝。

有三种颜色的球，算法的目标是将这三种球按颜色顺序正确地排列。它其实是三向切分快速排序的一种变种，在三向切分快速排序中，每次切分都将数组分成三个区间：小于切分元素、等于切分元素、大于切分元素，而该算法是将数组分成三个区间：等于红色、等于白色、等于蓝色。


1. 按颜色进行排序

75. Sort Colors (Medium)

Leetcode / 力扣

1
2
Input: [2,0,2,1,1,0]
Output: [0,0,1,1,2,2]

题目描述：只有 0/1/2 三种颜色。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public void sortColors(int[] nums) {
    int zero = -1, one = 0, two = nums.length;
    while (one < two) {
        if (nums[one] == 0) {
            swap(nums, ++zero, one++);
        } else if (nums[one] == 2) {
            swap(nums, --two, one);
        } else {
            ++one;
        }
    }
}

private void swap(int[] nums, int i, int j) {
    int t = nums[i];
    nums[i] = nums[j];
    nums[j] = t;
}

展开全文 >>

双指针

双指针主要用于遍历数组，两个指针指向不同的元素，从而协同完成任务。

1. 有序数组的 Two Sum

167. Two Sum II - Input array is sorted (Easy)

Leetcode / 力扣

1
2
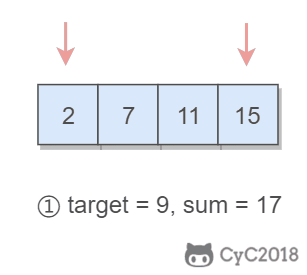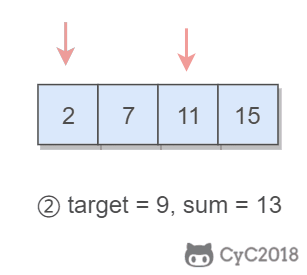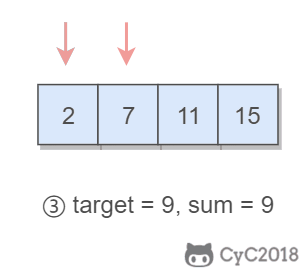
Input: numbers={2, 7, 11, 15}, target=9
Output: index1=1, index2=2

题目描述：在有序数组中找出两个数，使它们的和为 target。

使用双指针，一个指针指向值较小的元素，一个指针指向值较大的元素。指向较小元素的指针从头向尾遍历，指向较大元素的指针从尾向头遍历。

  • 如果两个指针指向元素的和 sum == target，那么得到要求的结果；
  • 如果 sum > target，移动较大的元素，使 sum 变小一些；
  • 如果 sum < target，移动较小的元素，使 sum 变大一些。

数组中的元素最多遍历一次，时间复杂度为 O(N)。只使用了两个额外变量，空间复杂度为 O(1)。


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int[] twoSum(int[] numbers, int target) {
    if (numbers == null) return null;
    int i = 0, j = numbers.length - 1;
    while (i < j) {
        int sum = numbers[i] + numbers[j];
        if (sum == target) {
            return new int[]{i + 1, j + 1};
        } else if (sum < target) {
            i++;
        } else {
            j--;
        }
    }
    return null;
}

2. 两数平方和

633. Sum of Square Numbers (Easy)

Leetcode / 力扣

1
2
3
Input: 5
Output: True
Explanation: 1 * 1 + 2 * 2 = 5

题目描述：判断一个非负整数是否为两个整数的平方和。

可以看成是在元素为 0~target 的有序数组中查找两个数，使得这两个数的平方和为 target，如果能找到，则返回 true，表示 target 是两个整数的平方和。

本题和 167. Two Sum II - Input array is sorted 类似，只有一个明显区别：一个是和为 target，一个是平方和为 target。本题同样可以使用双指针得到两个数，使其平方和为 target。

本题的关键是右指针的初始化，实现剪枝，从而降低时间复杂度。设右指针为 x，左指针固定为 0，为了使 02 + x2 的值尽可能接近 target，我们可以将 x 取为 sqrt(target)。

因为最多只需要遍历一次 0~sqrt(target)，所以时间复杂度为 O(sqrt(target))。又因为只使用了两个额外的变量，因此空间复杂度为 O(1)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public boolean judgeSquareSum(int target) {
    if (target < 0) return false;
    int i = 0, j = (int) Math.sqrt(target);
    while (i <= j) {
        int powSum = i * i + j * j;
        if (powSum == target) {
            return true;
        } else if (powSum > target) {
            j--;
        } else {
            i++;
        }
    }
    return false;
}

3. 反转字符串中的元音字符

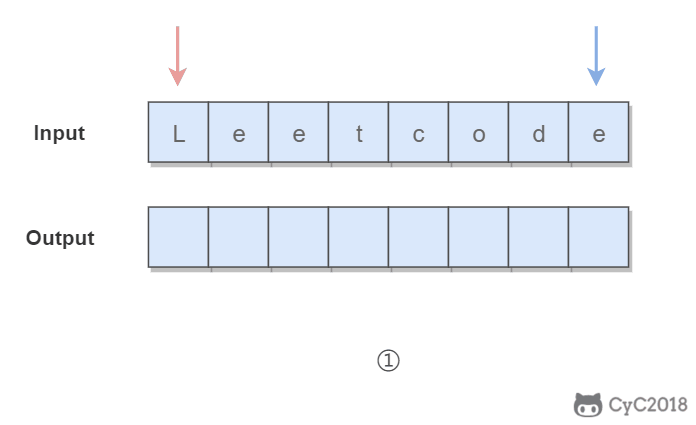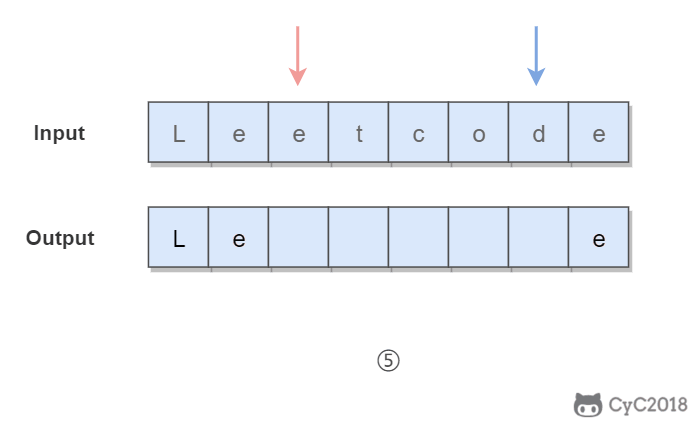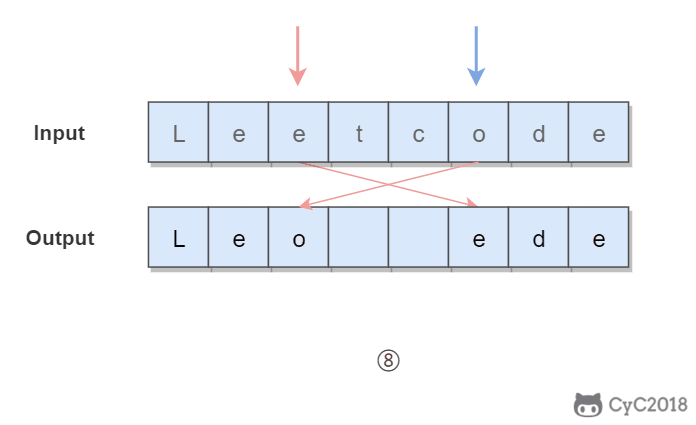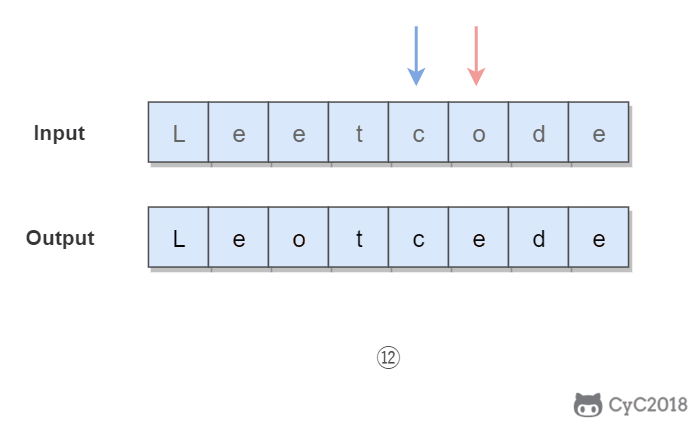
345. Reverse Vowels of a String (Easy)

Leetcode / 力扣

1
Given s = "leetcode", return "leotcede".

使用双指针，一个指针从头向尾遍历，一个指针从尾到头遍历，当两个指针都遍历到元音字符时，交换这两个元音字符。

为了快速判断一个字符是不是元音字符，我们将全部元音字符添加到集合 HashSet 中，从而以 O(1) 的时间复杂度进行该操作。

  • 时间复杂度为 O(N)：只需要遍历所有元素一次
  • 空间复杂度 O(1)：只需要使用两个额外变量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
private final static HashSet<Character> vowels = new HashSet<>(
        Arrays.asList('a', 'e', 'i', 'o', 'u', 'A', 'E', 'I', 'O', 'U'));

public String reverseVowels(String s) {
    if (s == null) return null;
    int i = 0, j = s.length() - 1;
    char[] result = new char[s.length()];
    while (i <= j) {
        char ci = s.charAt(i);
        char cj = s.charAt(j);
        if (!vowels.contains(ci)) {
            result[i++] = ci;
        } else if (!vowels.contains(cj)) {
            result[j--] = cj;
        } else {
            result[i++] = cj;
            result[j--] = ci;
        }
    }
    return new String(result);
}

4. 回文字符串

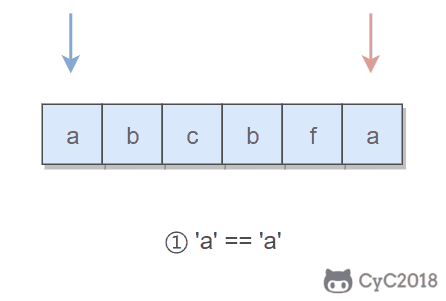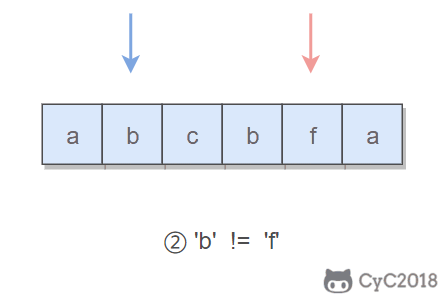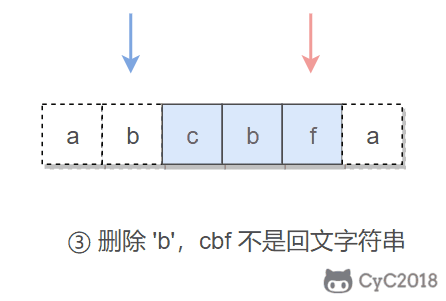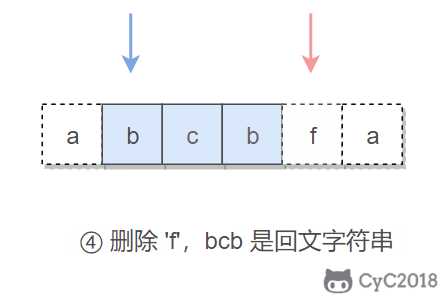
680. Valid Palindrome II (Easy)

Leetcode / 力扣

1
2
3
Input: "abca"
Output: True
Explanation: You could delete the character 'c'.

题目描述：可以删除一个字符，判断是否能构成回文字符串。

所谓的回文字符串，是指具有左右对称特点的字符串，例如 “abcba” 就是一个回文字符串。

使用双指针可以很容易判断一个字符串是否是回文字符串：令一个指针从左到右遍历，一个指针从右到左遍历，这两个指针同时移动一个位置，每次都判断两个指针指向的字符是否相同，如果都相同，字符串才是具有左右对称性质的回文字符串。


本题的关键是处理删除一个字符。在使用双指针遍历字符串时，如果出现两个指针指向的字符不相等的情况，我们就试着删除一个字符，再判断删除完之后的字符串是否是回文字符串。

在判断是否为回文字符串时，我们不需要判断整个字符串，因为左指针左边和右指针右边的字符之前已经判断过具有对称性质，所以只需要判断中间的子字符串即可。

在试着删除字符时，我们既可以删除左指针指向的字符，也可以删除右指针指向的字符。


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public boolean validPalindrome(String s) {
    for (int i = 0, j = s.length() - 1; i < j; i++, j--) {
        if (s.charAt(i) != s.charAt(j)) {
            return isPalindrome(s, i, j - 1) || isPalindrome(s, i + 1, j);
        }
    }
    return true;
}

private boolean isPalindrome(String s, int i, int j) {
    while (i < j) {
        if (s.charAt(i++) != s.charAt(j--)) {
            return false;
        }
    }
    return true;
}

5. 归并两个有序数组

88. Merge Sorted Array (Easy)

Leetcode / 力扣

1
2
3
4
5
Input:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6],       n = 3

Output: [1,2,2,3,5,6]

题目描述：把归并结果存到第一个数组上。

需要从尾开始遍历，否则在 nums1 上归并得到的值会覆盖还未进行归并比较的值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public void merge(int[] nums1, int m, int[] nums2, int n) {
    int index1 = m - 1, index2 = n - 1;
    int indexMerge = m + n - 1;
    while (index2 >= 0) {
        if (index1 < 0) {
            nums1[indexMerge--] = nums2[index2--];
        } else if (index2 < 0) {
            nums1[indexMerge--] = nums1[index1--];
        } else if (nums1[index1] > nums2[index2]) {
            nums1[indexMerge--] = nums1[index1--];
        } else {
            nums1[indexMerge--] = nums2[index2--];
        }
    }
}

6. 判断链表是否存在环

141. Linked List Cycle (Easy)

Leetcode / 力扣

使用双指针，一个指针每次移动一个节点，一个指针每次移动两个节点，如果存在环，那么这两个指针一定会相遇。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public boolean hasCycle(ListNode head) {
    if (head == null) {
        return false;
    }
    ListNode l1 = head, l2 = head.next;
    while (l1 != null && l2 != null && l2.next != null) {
        if (l1 == l2) {
            return true;
        }
        l1 = l1.next;
        l2 = l2.next.next;
    }
    return false;
}

7. 最长子序列

524. Longest Word in Dictionary through Deleting (Medium)

Leetcode / 力扣

1
2
3
4
5
Input:
s = "abpcplea", d = ["ale","apple","monkey","plea"]

Output:
"apple"

题目描述：删除 s 中的一些字符，使得它构成字符串列表 d 中的一个字符串，找出能构成的最长字符串。如果有多个相同长度的结果，返回字典序的最小字符串。

通过删除字符串 s 中的一个字符能得到字符串 t，可以认为 t 是 s 的子序列，我们可以使用双指针来判断一个字符串是否为另一个字符串的子序列。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public String findLongestWord(String s, List<String> d) {
    String longestWord = "";
    for (String target : d) {
        int l1 = longestWord.length(), l2 = target.length();
        if (l1 > l2 || (l1 == l2 && longestWord.compareTo(target) < 0)) {
            continue;
        }
        if (isSubstr(s, target)) {
            longestWord = target;
        }
    }
    return longestWord;
}

private boolean isSubstr(String s, String target) {
    int i = 0, j = 0;
    while (i < s.length() && j < target.length()) {
        if (s.charAt(i) == target.charAt(j)) {
            j++;
        }
        i++;
    }
    return j == target.length();
}

展开全文 >>

ElasticSearch

Elasticsearch 是一个实时的分布式搜索分析引擎，解决问题：

1、自动维护数据的分布到多个节点的索引的建立，还有搜索请求分布到多个节点的执行

2、自动维护数据的冗余副本，保证了一旦机器宕机，不会丢失数据

3、封装了更多高级的功能，例如聚合分析的功能，基于地理位置的搜索

more >>

展开全文 >>

树

递归

一棵树要么是空树，要么有两个指针，每个指针指向一棵树。树是一种递归结构，很多树的问题可以使用递归来处理。

1. 树的高度

104. Maximum Depth of Binary Tree (Easy)

Leetcode / 力扣

1
2
3
4
public int maxDepth(TreeNode root) {
    if (root == null) return 0;
    return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
}

2. 平衡树

110. Balanced Binary Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
  3
 / \
9  20
  /  \
 15   7

平衡树左右子树高度差都小于等于 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
private boolean result = true;

public boolean isBalanced(TreeNode root) {
    maxDepth(root);
    return result;
}

public int maxDepth(TreeNode root) {
    if (root == null) return 0;
    int l = maxDepth(root.left);
    int r = maxDepth(root.right);
    if (Math.abs(l - r) > 1) result = false;
    return 1 + Math.max(l, r);
}

3. 两节点的最长路径

543. Diameter of Binary Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
Input:

         1
        / \
       2  3
      / \
     4   5

Return 3, which is the length of the path [4,2,1,3] or [5,2,1,3].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
private int max = 0;

public int diameterOfBinaryTree(TreeNode root) {
    depth(root);
    return max;
}

private int depth(TreeNode root) {
    if (root == null) return 0;
    int leftDepth = depth(root.left);
    int rightDepth = depth(root.right);
    max = Math.max(max, leftDepth + rightDepth);
    return Math.max(leftDepth, rightDepth) + 1;
}

4. 翻转树

226. Invert Binary Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
public TreeNode invertTree(TreeNode root) {
    if (root == null) return null;
    TreeNode left = root.left;  // 后面的操作会改变 left 指针，因此先保存下来
    root.left = invertTree(root.right);
    root.right = invertTree(left);
    return root;
}

5. 归并两棵树

617. Merge Two Binary Trees (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Input:
       Tree 1                     Tree 2
          1                         2
         / \                       / \
        3   2                     1   3
       /                           \   \
      5                             4   7

Output:
         3
        / \
       4   5
      / \   \
     5   4   7
1
2
3
4
5
6
7
8
9
public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
    if (t1 == null && t2 == null) return null;
    if (t1 == null) return t2;
    if (t2 == null) return t1;
    TreeNode root = new TreeNode(t1.val + t2.val);
    root.left = mergeTrees(t1.left, t2.left);
    root.right = mergeTrees(t1.right, t2.right);
    return root;
}

6. 判断路径和是否等于一个数

Leetcdoe : 112. Path Sum (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
Given the below binary tree and sum = 22,

              5
             / \
            4   8
           /   / \
          11  13  4
         /  \      \
        7    2      1

return true, as there exist a root-to-leaf path 5->4->11->2 which sum is 22.

路径和定义为从 root 到 leaf 的所有节点的和。

1
2
3
4
5
public boolean hasPathSum(TreeNode root, int sum) {
    if (root == null) return false;
    if (root.left == null && root.right == null && root.val == sum) return true;
    return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
}

7. 统计路径和等于一个数的路径数量

437. Path Sum III (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8

      10
     /  \
    5   -3
   / \    \
  3   2   11
 / \   \
3  -2   1

Return 3. The paths that sum to 8 are:

1.  5 -> 3
2.  5 -> 2 -> 1
3. -3 -> 11

路径不一定以 root 开头，也不一定以 leaf 结尾，但是必须连续。

1
2
3
4
5
6
7
8
9
10
11
12
13
public int pathSum(TreeNode root, int sum) {
    if (root == null) return 0;
    int ret = pathSumStartWithRoot(root, sum) + pathSum(root.left, sum) + pathSum(root.right, sum);
    return ret;
}

private int pathSumStartWithRoot(TreeNode root, int sum) {
    if (root == null) return 0;
    int ret = 0;
    if (root.val == sum) ret++;
    ret += pathSumStartWithRoot(root.left, sum - root.val) + pathSumStartWithRoot(root.right, sum - root.val);
    return ret;
}

8. 子树

572. Subtree of Another Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Given tree s:
     3
    / \
   4   5
  / \
 1   2

Given tree t:
   4
  / \
 1   2

Return true, because t has the same structure and node values with a subtree of s.

Given tree s:

     3
    / \
   4   5
  / \
 1   2
    /
   0

Given tree t:
   4
  / \
 1   2

Return false.
1
2
3
4
5
6
7
8
9
10
11
public boolean isSubtree(TreeNode s, TreeNode t) {
    if (s == null) return false;
    return isSubtreeWithRoot(s, t) || isSubtree(s.left, t) || isSubtree(s.right, t);
}

private boolean isSubtreeWithRoot(TreeNode s, TreeNode t) {
    if (t == null && s == null) return true;
    if (t == null || s == null) return false;
    if (t.val != s.val) return false;
    return isSubtreeWithRoot(s.left, t.left) && isSubtreeWithRoot(s.right, t.right);
}

9. 树的对称

101. Symmetric Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
    1
   / \
  2   2
 / \ / \
3  4 4  3
1
2
3
4
5
6
7
8
9
10
11
public boolean isSymmetric(TreeNode root) {
    if (root == null) return true;
    return isSymmetric(root.left, root.right);
}

private boolean isSymmetric(TreeNode t1, TreeNode t2) {
    if (t1 == null && t2 == null) return true;
    if (t1 == null || t2 == null) return false;
    if (t1.val != t2.val) return false;
    return isSymmetric(t1.left, t2.right) && isSymmetric(t1.right, t2.left);
}

10. 最小路径

111. Minimum Depth of Binary Tree (Easy)

Leetcode / 力扣

树的根节点到叶子节点的最小路径长度

1
2
3
4
5
6
7
public int minDepth(TreeNode root) {
    if (root == null) return 0;
    int left = minDepth(root.left);
    int right = minDepth(root.right);
    if (left == 0 || right == 0) return left + right + 1;
    return Math.min(left, right) + 1;
}

11. 统计左叶子节点的和

404. Sum of Left Leaves (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
    3
   / \
  9  20
    /  \
   15   7

There are two left leaves in the binary tree, with values 9 and 15 respectively. Return 24.
1
2
3
4
5
6
7
8
9
10
public int sumOfLeftLeaves(TreeNode root) {
    if (root == null) return 0;
    if (isLeaf(root.left)) return root.left.val + sumOfLeftLeaves(root.right);
    return sumOfLeftLeaves(root.left) + sumOfLeftLeaves(root.right);
}

private boolean isLeaf(TreeNode node){
    if (node == null) return false;
    return node.left == null && node.right == null;
}

12. 相同节点值的最大路径长度

687. Longest Univalue Path (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
             1
            / \
           4   5
          / \   \
         4   4   5

Output : 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
private int path = 0;

public int longestUnivaluePath(TreeNode root) {
    dfs(root);
    return path;
}

private int dfs(TreeNode root){
    if (root == null) return 0;
    int left = dfs(root.left);
    int right = dfs(root.right);
    int leftPath = root.left != null && root.left.val == root.val ? left + 1 : 0;
    int rightPath = root.right != null && root.right.val == root.val ? right + 1 : 0;
    path = Math.max(path, leftPath + rightPath);
    return Math.max(leftPath, rightPath);
}

13. 间隔遍历

337. House Robber III (Medium)

Leetcode / 力扣

1
2
3
4
5
6
     3
    / \
   2   3
    \   \
     3   1
Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.
1
2
3
4
5
6
7
8
9
10
11
12
13
Map<TreeNode, Integer> cache = new HashMap<>(); 

public int rob(TreeNode root) {
    if (root == null) return 0;
    if (cache.containsKey(root)) return cache.get(root);
    int val1 = root.val;
    if (root.left != null) val1 += rob(root.left.left) + rob(root.left.right);
    if (root.right != null) val1 += rob(root.right.left) + rob(root.right.right);
    int val2 = rob(root.left) + rob(root.right);
    int res = Math.max(val1, val2);
    cache.put(root, res);
    return res;
}

14. 找出二叉树中第二小的节点

671. Second Minimum Node In a Binary Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
Input:
   2
  / \
 2   5
    / \
    5  7

Output: 5

一个节点要么具有 0 个或 2 个子节点，如果有子节点，那么根节点是最小的节点。

1
2
3
4
5
6
7
8
9
10
11
public int findSecondMinimumValue(TreeNode root) {
    if (root == null) return -1;
    if (root.left == null && root.right == null) return -1;
    int leftVal = root.left.val;
    int rightVal = root.right.val;
    if (leftVal == root.val) leftVal = findSecondMinimumValue(root.left);
    if (rightVal == root.val) rightVal = findSecondMinimumValue(root.right);
    if (leftVal != -1 && rightVal != -1) return Math.min(leftVal, rightVal);
    if (leftVal != -1) return leftVal;
    return rightVal;
}

层次遍历

使用 BFS 进行层次遍历。不需要使用两个队列来分别存储当前层的节点和下一层的节点，因为在开始遍历一层的节点时，当前队列中的节点数就是当前层的节点数，只要控制遍历这么多节点数，就能保证这次遍历的都是当前层的节点。

1. 一棵树每层节点的平均数

637. Average of Levels in Binary Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public List<Double> averageOfLevels(TreeNode root) {
    List<Double> ret = new ArrayList<>();
    if (root == null) return ret;
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    while (!queue.isEmpty()) {
        int cnt = queue.size();
        double sum = 0;
        for (int i = 0; i < cnt; i++) {
            TreeNode node = queue.poll();
            sum += node.val;
            if (node.left != null) queue.add(node.left);
            if (node.right != null) queue.add(node.right);
        }
        ret.add(sum / cnt);
    }
    return ret;
}

2. 得到左下角的节点

513. Find Bottom Left Tree Value (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
Input:

        1
       / \
      2   3
     /   / \
    4   5   6
       /
      7

Output:
7
1
2
3
4
5
6
7
8
9
10
public int findBottomLeftValue(TreeNode root) {
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(root);
    while (!queue.isEmpty()) {
        root = queue.poll();
        if (root.right != null) queue.add(root.right);
        if (root.left != null) queue.add(root.left);
    }
    return root.val;
}

前中后序遍历

1
2
3
4
5
    1
   / \
  2   3
 / \   \
4   5   6
  • 层次遍历顺序：[1 2 3 4 5 6]
  • 前序遍历顺序：[1 2 4 5 3 6]
  • 中序遍历顺序：[4 2 5 1 3 6]
  • 后序遍历顺序：[4 5 2 6 3 1]

层次遍历使用 BFS 实现，利用的就是 BFS 一层一层遍历的特性；而前序、中序、后序遍历利用了 DFS 实现。

前序、中序、后序遍只是在对节点访问的顺序有一点不同，其它都相同。

① 前序

1
2
3
4
5
void dfs(TreeNode root) {
    visit(root);
    dfs(root.left);
    dfs(root.right);
}

② 中序

1
2
3
4
5
void dfs(TreeNode root) {
    dfs(root.left);
    visit(root);
    dfs(root.right);
}

③ 后序

1
2
3
4
5
void dfs(TreeNode root) {
    dfs(root.left);
    dfs(root.right);
    visit(root);
}

1. 非递归实现二叉树的前序遍历

144. Binary Tree Preorder Traversal (Medium)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
13
public List<Integer> preorderTraversal(TreeNode root) {
    List<Integer> ret = new ArrayList<>();
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        TreeNode node = stack.pop();
        if (node == null) continue;
        ret.add(node.val);
        stack.push(node.right);  // 先右后左，保证左子树先遍历
        stack.push(node.left);
    }
    return ret;
}

2. 非递归实现二叉树的后序遍历

145. Binary Tree Postorder Traversal (Medium)

Leetcode / 力扣

前序遍历为 root -> left -> right，后序遍历为 left -> right -> root。可以修改前序遍历成为 root -> right -> left，那么这个顺序就和后序遍历正好相反。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public List<Integer> postorderTraversal(TreeNode root) {
    List<Integer> ret = new ArrayList<>();
    Stack<TreeNode> stack = new Stack<>();
    stack.push(root);
    while (!stack.isEmpty()) {
        TreeNode node = stack.pop();
        if (node == null) continue;
        ret.add(node.val);
        stack.push(node.left);
        stack.push(node.right);
    }
    Collections.reverse(ret);
    return ret;
}

3. 非递归实现二叉树的中序遍历

94. Binary Tree Inorder Traversal (Medium)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public List<Integer> inorderTraversal(TreeNode root) {
    List<Integer> ret = new ArrayList<>();
    if (root == null) return ret;
    Stack<TreeNode> stack = new Stack<>();
    TreeNode cur = root;
    while (cur != null || !stack.isEmpty()) {
        while (cur != null) {
            stack.push(cur);
            cur = cur.left;
        }
        TreeNode node = stack.pop();
        ret.add(node.val);
        cur = node.right;
    }
    return ret;
}

BST

二叉查找树（BST）：根节点大于等于左子树所有节点，小于等于右子树所有节点。

二叉查找树中序遍历有序。

1. 修剪二叉查找树

669. Trim a Binary Search Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Input:

    3
   / \
  0   4
   \
    2
   /
  1

  L = 1
  R = 3

Output:

      3
     /
   2
  /
 1

题目描述：只保留值在 L ~ R 之间的节点

1
2
3
4
5
6
7
8
public TreeNode trimBST(TreeNode root, int L, int R) {
    if (root == null) return null;
    if (root.val > R) return trimBST(root.left, L, R);
    if (root.val < L) return trimBST(root.right, L, R);
    root.left = trimBST(root.left, L, R);
    root.right = trimBST(root.right, L, R);
    return root;
}

2. 寻找二叉查找树的第 k 个元素

230. Kth Smallest Element in a BST (Medium)

Leetcode / 力扣

中序遍历解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
private int cnt = 0;
private int val;

public int kthSmallest(TreeNode root, int k) {
    inOrder(root, k);
    return val;
}

private void inOrder(TreeNode node, int k) {
    if (node == null) return;
    inOrder(node.left, k);
    cnt++;
    if (cnt == k) {
        val = node.val;
        return;
    }
    inOrder(node.right, k);
}

递归解法：

1
2
3
4
5
6
7
8
9
10
11
public int kthSmallest(TreeNode root, int k) {
    int leftCnt = count(root.left);
    if (leftCnt == k - 1) return root.val;
    if (leftCnt > k - 1) return kthSmallest(root.left, k);
    return kthSmallest(root.right, k - leftCnt - 1);
}

private int count(TreeNode node) {
    if (node == null) return 0;
    return 1 + count(node.left) + count(node.right);
}

3. 把二叉查找树每个节点的值都加上比它大的节点的值

Convert BST to Greater Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
Input: The root of a Binary Search Tree like this:

              5
            /   \
           2     13

Output: The root of a Greater Tree like this:

             18
            /   \
          20     13

先遍历右子树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
private int sum = 0;

public TreeNode convertBST(TreeNode root) {
    traver(root);
    return root;
}

private void traver(TreeNode node) {
    if (node == null) return;
    traver(node.right);
    sum += node.val;
    node.val = sum;
    traver(node.left);
}

4. 二叉查找树的最近公共祖先

235. Lowest Common Ancestor of a Binary Search Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
        _______6______
      /                \
  ___2__             ___8__
 /      \           /      \
0        4         7        9
        /  \
       3   5

For example, the lowest common ancestor (LCA) of nodes 2 and 8 is 6. Another example is LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
1
2
3
4
5
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if (root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left, p, q);
    if (root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right, p, q);
    return root;
}

5. 二叉树的最近公共祖先

236. Lowest Common Ancestor of a Binary Tree (Medium)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
       _______3______
      /              \
  ___5__           ___1__
 /      \         /      \
6        2       0        8
        /  \
       7    4

For example, the lowest common ancestor (LCA) of nodes 5 and 1 is 3. Another example is LCA of nodes 5 and 4 is 5, since a node can be a descendant of itself according to the LCA definition.
1
2
3
4
5
6
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
    if (root == null || root == p || root == q) return root;
    TreeNode left = lowestCommonAncestor(root.left, p, q);
    TreeNode right = lowestCommonAncestor(root.right, p, q);
    return left == null ? right : right == null ? left : root;
}

6. 从有序数组中构造二叉查找树

108. Convert Sorted Array to Binary Search Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
public TreeNode sortedArrayToBST(int[] nums) {
    return toBST(nums, 0, nums.length - 1);
}

private TreeNode toBST(int[] nums, int sIdx, int eIdx){
    if (sIdx > eIdx) return null;
    int mIdx = (sIdx + eIdx) / 2;
    TreeNode root = new TreeNode(nums[mIdx]);
    root.left =  toBST(nums, sIdx, mIdx - 1);
    root.right = toBST(nums, mIdx + 1, eIdx);
    return root;
}

7. 根据有序链表构造平衡的二叉查找树

109. Convert Sorted List to Binary Search Tree (Medium)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
Given the sorted linked list: [-10,-3,0,5,9],

One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:

      0
     / \
   -3   9
   /   /
 -10  5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public TreeNode sortedListToBST(ListNode head) {
    if (head == null) return null;
    if (head.next == null) return new TreeNode(head.val);
    ListNode preMid = preMid(head);
    ListNode mid = preMid.next;
    preMid.next = null;  // 断开链表
    TreeNode t = new TreeNode(mid.val);
    t.left = sortedListToBST(head);
    t.right = sortedListToBST(mid.next);
    return t;
}

private ListNode preMid(ListNode head) {
    ListNode slow = head, fast = head.next;
    ListNode pre = head;
    while (fast != null && fast.next != null) {
        pre = slow;
        slow = slow.next;
        fast = fast.next.next;
    }
    return pre;
}

8. 在二叉查找树中寻找两个节点，使它们的和为一个给定值

653. Two Sum IV - Input is a BST (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
Input:

    5
   / \
  3   6
 / \   \
2   4   7

Target = 9

Output: True

使用中序遍历得到有序数组之后，再利用双指针对数组进行查找。

应该注意到，这一题不能用分别在左右子树两部分来处理这种思想，因为两个待求的节点可能分别在左右子树中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public boolean findTarget(TreeNode root, int k) {
    List<Integer> nums = new ArrayList<>();
    inOrder(root, nums);
    int i = 0, j = nums.size() - 1;
    while (i < j) {
        int sum = nums.get(i) + nums.get(j);
        if (sum == k) return true;
        if (sum < k) i++;
        else j--;
    }
    return false;
}

private void inOrder(TreeNode root, List<Integer> nums) {
    if (root == null) return;
    inOrder(root.left, nums);
    nums.add(root.val);
    inOrder(root.right, nums);
}

9. 在二叉查找树中查找两个节点之差的最小绝对值

530. Minimum Absolute Difference in BST (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
Input:

   1
    \
     3
    /
   2

Output:

1

利用二叉查找树的中序遍历为有序的性质，计算中序遍历中临近的两个节点之差的绝对值，取最小值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
private int minDiff = Integer.MAX_VALUE;
private TreeNode preNode = null;

public int getMinimumDifference(TreeNode root) {
    inOrder(root);
    return minDiff;
}

private void inOrder(TreeNode node) {
    if (node == null) return;
    inOrder(node.left);
    if (preNode != null) minDiff = Math.min(minDiff, node.val - preNode.val);
    preNode = node;
    inOrder(node.right);
}

10. 寻找二叉查找树中出现次数最多的值

501. Find Mode in Binary Search Tree (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
   1
    \
     2
    /
   2

return [2].

答案可能不止一个，也就是有多个值出现的次数一样多。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
private int curCnt = 1;
private int maxCnt = 1;
private TreeNode preNode = null;

public int[] findMode(TreeNode root) {
    List<Integer> maxCntNums = new ArrayList<>();
    inOrder(root, maxCntNums);
    int[] ret = new int[maxCntNums.size()];
    int idx = 0;
    for (int num : maxCntNums) {
        ret[idx++] = num;
    }
    return ret;
}

private void inOrder(TreeNode node, List<Integer> nums) {
    if (node == null) return;
    inOrder(node.left, nums);
    if (preNode != null) {
        if (preNode.val == node.val) curCnt++;
        else curCnt = 1;
    }
    if (curCnt > maxCnt) {
        maxCnt = curCnt;
        nums.clear();
        nums.add(node.val);
    } else if (curCnt == maxCnt) {
        nums.add(node.val);
    }
    preNode = node;
    inOrder(node.right, nums);
}

Trie


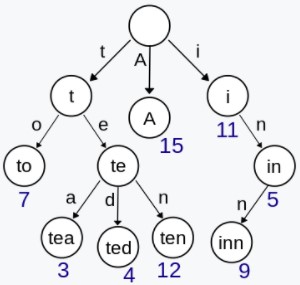
Trie，又称前缀树或字典树，用于判断字符串是否存在或者是否具有某种字符串前缀。

1. 实现一个 Trie

208. Implement Trie (Prefix Tree) (Medium)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
class Trie {

    private class Node {
        Node[] childs = new Node[26];
        boolean isLeaf;
    }

    private Node root = new Node();

    public Trie() {
    }

    public void insert(String word) {
        insert(word, root);
    }

    private void insert(String word, Node node) {
        if (node == null) return;
        if (word.length() == 0) {
            node.isLeaf = true;
            return;
        }
        int index = indexForChar(word.charAt(0));
        if (node.childs[index] == null) {
            node.childs[index] = new Node();
        }
        insert(word.substring(1), node.childs[index]);
    }

    public boolean search(String word) {
        return search(word, root);
    }

    private boolean search(String word, Node node) {
        if (node == null) return false;
        if (word.length() == 0) return node.isLeaf;
        int index = indexForChar(word.charAt(0));
        return search(word.substring(1), node.childs[index]);
    }

    public boolean startsWith(String prefix) {
        return startWith(prefix, root);
    }

    private boolean startWith(String prefix, Node node) {
        if (node == null) return false;
        if (prefix.length() == 0) return true;
        int index = indexForChar(prefix.charAt(0));
        return startWith(prefix.substring(1), node.childs[index]);
    }

    private int indexForChar(char c) {
        return c - 'a';
    }
}

2. 实现一个 Trie，用来求前缀和

677. Map Sum Pairs (Medium)

Leetcode / 力扣

1
2
3
4
Input: insert("apple", 3), Output: Null
Input: sum("ap"), Output: 3
Input: insert("app", 2), Output: Null
Input: sum("ap"), Output: 5
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class MapSum {

    private class Node {
        Node[] child = new Node[26];
        int value;
    }

    private Node root = new Node();

    public MapSum() {

    }

    public void insert(String key, int val) {
        insert(key, root, val);
    }

    private void insert(String key, Node node, int val) {
        if (node == null) return;
        if (key.length() == 0) {
            node.value = val;
            return;
        }
        int index = indexForChar(key.charAt(0));
        if (node.child[index] == null) {
            node.child[index] = new Node();
        }
        insert(key.substring(1), node.child[index], val);
    }

    public int sum(String prefix) {
        return sum(prefix, root);
    }

    private int sum(String prefix, Node node) {
        if (node == null) return 0;
        if (prefix.length() != 0) {
            int index = indexForChar(prefix.charAt(0));
            return sum(prefix.substring(1), node.child[index]);
        }
        int sum = node.value;
        for (Node child : node.child) {
            sum += sum(prefix, child);
        }
        return sum;
    }

    private int indexForChar(char c) {
        return c - 'a';
    }
}

展开全文 >>

数组与矩阵

1. 把数组中的 0 移到末尾

283. Move Zeroes (Easy)

Leetcode / 力扣

1
For example, given nums = [0, 1, 0, 3, 12], after calling your function, nums should be [1, 3, 12, 0, 0].
1
2
3
4
5
6
7
8
9
10
11
public void moveZeroes(int[] nums) {
    int idx = 0;
    for (int num : nums) {
        if (num != 0) {
            nums[idx++] = num;
        }
    }
    while (idx < nums.length) {
        nums[idx++] = 0;
    }
}

2. 改变矩阵维度

566. Reshape the Matrix (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
Input:
nums =
[[1,2],
 [3,4]]
r = 1, c = 4

Output:
[[1,2,3,4]]

Explanation:
The row-traversing of nums is [1,2,3,4]. The new reshaped matrix is a 1 * 4 matrix, fill it row by row by using the previous list.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int[][] matrixReshape(int[][] nums, int r, int c) {
    int m = nums.length, n = nums[0].length;
    if (m * n != r * c) {
        return nums;
    }
    int[][] reshapedNums = new int[r][c];
    int index = 0;
    for (int i = 0; i < r; i++) {
        for (int j = 0; j < c; j++) {
            reshapedNums[i][j] = nums[index / n][index % n];
            index++;
        }
    }
    return reshapedNums;
}

3. 找出数组中最长的连续 1

485. Max Consecutive Ones (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
public int findMaxConsecutiveOnes(int[] nums) {
    int max = 0, cur = 0;
    for (int x : nums) {
        cur = x == 0 ? 0 : cur + 1;
        max = Math.max(max, cur);
    }
    return max;
}

4. 有序矩阵查找

240. Search a 2D Matrix II (Medium)

Leetcode / 力扣

1
2
3
4
5
[
   [ 1,  5,  9],
   [10, 11, 13],
   [12, 13, 15]
]
1
2
3
4
5
6
7
8
9
10
11
public boolean searchMatrix(int[][] matrix, int target) {
    if (matrix == null || matrix.length == 0 || matrix[0].length == 0) return false;
    int m = matrix.length, n = matrix[0].length;
    int row = 0, col = n - 1;
    while (row < m && col >= 0) {
        if (target == matrix[row][col]) return true;
        else if (target < matrix[row][col]) col--;
        else row++;
    }
    return false;
}

5. 有序矩阵的 Kth Element

378. Kth Smallest Element in a Sorted Matrix ((Medium))

Leetcode / 力扣

1
2
3
4
5
6
7
8
matrix = [
  [ 1,  5,  9],
  [10, 11, 13],
  [12, 13, 15]
],
k = 8,

return 13.

解题参考：Share my thoughts and Clean Java Code

二分查找解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public int kthSmallest(int[][] matrix, int k) {
    int m = matrix.length, n = matrix[0].length;
    int lo = matrix[0][0], hi = matrix[m - 1][n - 1];
    while (lo <= hi) {
        int mid = lo + (hi - lo) / 2;
        int cnt = 0;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n && matrix[i][j] <= mid; j++) {
                cnt++;
            }
        }
        if (cnt < k) lo = mid + 1;
        else hi = mid - 1;
    }
    return lo;
}

堆解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public int kthSmallest(int[][] matrix, int k) {
    int m = matrix.length, n = matrix[0].length;
    PriorityQueue<Tuple> pq = new PriorityQueue<Tuple>();
    for(int j = 0; j < n; j++) pq.offer(new Tuple(0, j, matrix[0][j]));
    for(int i = 0; i < k - 1; i++) { // 小根堆，去掉 k - 1 个堆顶元素，此时堆顶元素就是第 k 的数
        Tuple t = pq.poll();
        if(t.x == m - 1) continue;
        pq.offer(new Tuple(t.x + 1, t.y, matrix[t.x + 1][t.y]));
    }
    return pq.poll().val;
}

class Tuple implements Comparable<Tuple> {
    int x, y, val;
    public Tuple(int x, int y, int val) {
        this.x = x; this.y = y; this.val = val;
    }

    @Override
    public int compareTo(Tuple that) {
        return this.val - that.val;
    }
}

6. 一个数组元素在 [1, n] 之间，其中一个数被替换为另一个数，找出重复的数和丢失的数

645. Set Mismatch (Easy)

Leetcode / 力扣

1
2
Input: nums = [1,2,2,4]
Output: [2,3]
1
2
Input: nums = [1,2,2,4]
Output: [2,3]

最直接的方法是先对数组进行排序，这种方法时间复杂度为 O(NlogN)。本题可以以 O(N) 的时间复杂度、O(1) 空间复杂度来求解。

主要思想是通过交换数组元素，使得数组上的元素在正确的位置上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public int[] findErrorNums(int[] nums) {
    for (int i = 0; i < nums.length; i++) {
        while (nums[i] != i + 1 && nums[nums[i] - 1] != nums[i]) {
            swap(nums, i, nums[i] - 1);
        }
    }
    for (int i = 0; i < nums.length; i++) {
        if (nums[i] != i + 1) {
            return new int[]{nums[i], i + 1};
        }
    }
    return null;
}

private void swap(int[] nums, int i, int j) {
    int tmp = nums[i];
    nums[i] = nums[j];
    nums[j] = tmp;
}

7. 找出数组中重复的数，数组值在 [1, n] 之间

287. Find the Duplicate Number (Medium)

Leetcode / 力扣

要求不能修改数组，也不能使用额外的空间。

二分查找解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
public int findDuplicate(int[] nums) {
     int l = 1, h = nums.length - 1;
     while (l <= h) {
         int mid = l + (h - l) / 2;
         int cnt = 0;
         for (int i = 0; i < nums.length; i++) {
             if (nums[i] <= mid) cnt++;
         }
         if (cnt > mid) h = mid - 1;
         else l = mid + 1;
     }
     return l;
}

双指针解法，类似于有环链表中找出环的入口：

1
2
3
4
5
6
7
8
9
10
11
12
13
public int findDuplicate(int[] nums) {
    int slow = nums[0], fast = nums[nums[0]];
    while (slow != fast) {
        slow = nums[slow];
        fast = nums[nums[fast]];
    }
    fast = 0;
    while (slow != fast) {
        slow = nums[slow];
        fast = nums[fast];
    }
    return slow;
}

8. 数组相邻差值的个数

667. Beautiful Arrangement II (Medium)

Leetcode / 力扣

1
2
3
Input: n = 3, k = 2
Output: [1, 3, 2]
Explanation: The [1, 3, 2] has three different positive integers ranging from 1 to 3, and the [2, 1] has exactly 2 distinct integers: 1 and 2.

题目描述：数组元素为 1~n 的整数，要求构建数组，使得相邻元素的差值不相同的个数为 k。

让前 k+1 个元素构建出 k 个不相同的差值，序列为：1 k+1 2 k 3 k-1 … k/2 k/2+1.

1
2
3
4
5
6
7
8
9
10
11
public int[] constructArray(int n, int k) {
    int[] ret = new int[n];
    ret[0] = 1;
    for (int i = 1, interval = k; i <= k; i++, interval--) {
        ret[i] = i % 2 == 1 ? ret[i - 1] + interval : ret[i - 1] - interval;
    }
    for (int i = k + 1; i < n; i++) {
        ret[i] = i + 1;
    }
    return ret;
}

9. 数组的度

697. Degree of an Array (Easy)

Leetcode / 力扣

1
2
Input: [1,2,2,3,1,4,2]
Output: 6

题目描述：数组的度定义为元素出现的最高频率，例如上面的数组度为 3。要求找到一个最小的子数组，这个子数组的度和原数组一样。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public int findShortestSubArray(int[] nums) {
    Map<Integer, Integer> numsCnt = new HashMap<>();
    Map<Integer, Integer> numsLastIndex = new HashMap<>();
    Map<Integer, Integer> numsFirstIndex = new HashMap<>();
    for (int i = 0; i < nums.length; i++) {
        int num = nums[i];
        numsCnt.put(num, numsCnt.getOrDefault(num, 0) + 1);
        numsLastIndex.put(num, i);
        if (!numsFirstIndex.containsKey(num)) {
            numsFirstIndex.put(num, i);
        }
    }
    int maxCnt = 0;
    for (int num : nums) {
        maxCnt = Math.max(maxCnt, numsCnt.get(num));
    }
    int ret = nums.length;
    for (int i = 0; i < nums.length; i++) {
        int num = nums[i];
        int cnt = numsCnt.get(num);
        if (cnt != maxCnt) continue;
        ret = Math.min(ret, numsLastIndex.get(num) - numsFirstIndex.get(num) + 1);
    }
    return ret;
}

10. 对角元素相等的矩阵

766. Toeplitz Matrix (Easy)

Leetcode / 力扣

1
2
3
4
5
1234
5123
9512

In the above grid, the diagonals are "[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]", and in each diagonal all elements are the same, so the answer is True.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public boolean isToeplitzMatrix(int[][] matrix) {
    for (int i = 0; i < matrix[0].length; i++) {
        if (!check(matrix, matrix[0][i], 0, i)) {
            return false;
        }
    }
    for (int i = 0; i < matrix.length; i++) {
        if (!check(matrix, matrix[i][0], i, 0)) {
            return false;
        }
    }
    return true;
}

private boolean check(int[][] matrix, int expectValue, int row, int col) {
    if (row >= matrix.length || col >= matrix[0].length) {
        return true;
    }
    if (matrix[row][col] != expectValue) {
        return false;
    }
    return check(matrix, expectValue, row + 1, col + 1);
}

11. 嵌套数组

565. Array Nesting (Medium)

Leetcode / 力扣

1
2
3
4
5
6
7
Input: A = [5,4,0,3,1,6,2]
Output: 4
Explanation:
A[0] = 5, A[1] = 4, A[2] = 0, A[3] = 3, A[4] = 1, A[5] = 6, A[6] = 2.

One of the longest S[K]:
S[0] = {A[0], A[5], A[6], A[2]} = {5, 6, 2, 0}

题目描述：S[i] 表示一个集合，集合的第一个元素是 A[i]，第二个元素是 A[A[i]]，如此嵌套下去。求最大的 S[i]。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int arrayNesting(int[] nums) {
    int max = 0;
    for (int i = 0; i < nums.length; i++) {
        int cnt = 0;
        for (int j = i; nums[j] != -1; ) {
            cnt++;
            int t = nums[j];
            nums[j] = -1; // 标记该位置已经被访问
            j = t;

        }
        max = Math.max(max, cnt);
    }
    return max;
}

12. 分隔数组

769. Max Chunks To Make Sorted (Medium)

Leetcode / 力扣

1
2
3
4
5
Input: arr = [1,0,2,3,4]
Output: 4
Explanation:
We can split into two chunks, such as [1, 0], [2, 3, 4].
However, splitting into [1, 0], [2], [3], [4] is the highest number of chunks possible.

题目描述：分隔数组，使得对每部分排序后数组就为有序。

1
2
3
4
5
6
7
8
9
10
public int maxChunksToSorted(int[] arr) {
    if (arr == null) return 0;
    int ret = 0;
    int right = arr[0];
    for (int i = 0; i < arr.length; i++) {
        right = Math.max(right, arr[i]);
        if (right == i) ret++;
    }
    return ret;
}

展开全文 >>

链表

链表是空节点，或者有一个值和一个指向下一个链表的指针，因此很多链表问题可以用递归来处理。

1. 找出两个链表的交点

160. Intersection of Two Linked Lists (Easy)

Leetcode / 力扣

例如以下示例中 A 和 B 两个链表相交于 c1：

1
2
3
4
5
A:          a1 → a2
                    ↘
                      c1 → c2 → c3
                    ↗
B:    b1 → b2 → b3

但是不会出现以下相交的情况，因为每个节点只有一个 next 指针，也就只能有一个后继节点，而以下示例中节点 c 有两个后继节点。

1
2
3
4
5
A:          a1 → a2       d1 → d2
                    ↘  ↗
                      c
                    ↗  ↘
B:    b1 → b2 → b3        e1 → e2

要求时间复杂度为 O(N)，空间复杂度为 O(1)。如果不存在交点则返回 null。

设 A 的长度为 a + c，B 的长度为 b + c，其中 c 为尾部公共部分长度，可知 a + c + b = b + c + a。

当访问 A 链表的指针访问到链表尾部时，令它从链表 B 的头部开始访问链表 B；同样地，当访问 B 链表的指针访问到链表尾部时，令它从链表 A 的头部开始访问链表 A。这样就能控制访问 A 和 B 两个链表的指针能同时访问到交点。

如果不存在交点，那么 a + b = b + a，以下实现代码中 l1 和 l2 会同时为 null，从而退出循环。

1
2
3
4
5
6
7
8
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
    ListNode l1 = headA, l2 = headB;
    while (l1 != l2) {
        l1 = (l1 == null) ? headB : l1.next;
        l2 = (l2 == null) ? headA : l2.next;
    }
    return l1;
}

如果只是判断是否存在交点，那么就是另一个问题，即 编程之美 3.6 的问题。有两种解法：

  • 把第一个链表的结尾连接到第二个链表的开头，看第二个链表是否存在环；
  • 或者直接比较两个链表的最后一个节点是否相同。

2. 链表反转

206. Reverse Linked List (Easy)

Leetcode / 力扣

递归

1
2
3
4
5
6
7
8
9
10
public ListNode reverseList(ListNode head) {
    if (head == null || head.next == null) {
        return head;
    }
    ListNode next = head.next;
    ListNode newHead = reverseList(next);
    next.next = head;
    head.next = null;
    return newHead;
}

头插法

1
2
3
4
5
6
7
8
9
10
public ListNode reverseList(ListNode head) {
    ListNode newHead = new ListNode(-1);
    while (head != null) {
        ListNode next = head.next;
        head.next = newHead.next;
        newHead.next = head;
        head = next;
    }
    return newHead.next;
}

3. 归并两个有序的链表

21. Merge Two Sorted Lists (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
10
11
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
    if (l1 == null) return l2;
    if (l2 == null) return l1;
    if (l1.val < l2.val) {
        l1.next = mergeTwoLists(l1.next, l2);
        return l1;
    } else {
        l2.next = mergeTwoLists(l1, l2.next);
        return l2;
    }
}

4. 从有序链表中删除重复节点

83. Remove Duplicates from Sorted List (Easy)

Leetcode / 力扣

1
2
Given 1->1->2, return 1->2.
Given 1->1->2->3->3, return 1->2->3.
1
2
3
4
5
public ListNode deleteDuplicates(ListNode head) {
    if (head == null || head.next == null) return head;
    head.next = deleteDuplicates(head.next);
    return head.val == head.next.val ? head.next : head;
}

5. 删除链表的倒数第 n 个节点

19. Remove Nth Node From End of List (Medium)

Leetcode / 力扣

1
2
Given linked list: 1->2->3->4->5, and n = 2.
After removing the second node from the end, the linked list becomes 1->2->3->5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public ListNode removeNthFromEnd(ListNode head, int n) {
    ListNode fast = head;
    while (n-- > 0) {
        fast = fast.next;
    }
    if (fast == null) return head.next;
    ListNode slow = head;
    while (fast.next != null) {
        fast = fast.next;
        slow = slow.next;
    }
    slow.next = slow.next.next;
    return head;
}

6. 交换链表中的相邻结点

24. Swap Nodes in Pairs (Medium)

Leetcode / 力扣

1
Given 1->2->3->4, you should return the list as 2->1->4->3.

题目要求：不能修改结点的 val 值，O(1) 空间复杂度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public ListNode swapPairs(ListNode head) {
    ListNode node = new ListNode(-1);
    node.next = head;
    ListNode pre = node;
    while (pre.next != null && pre.next.next != null) {
        ListNode l1 = pre.next, l2 = pre.next.next;
        ListNode next = l2.next;
        l1.next = next;
        l2.next = l1;
        pre.next = l2;

        pre = l1;
    }
    return node.next;
}

7. 链表求和

445. Add Two Numbers II (Medium)

Leetcode / 力扣

1
2
Input: (7 -> 2 -> 4 -> 3) + (5 -> 6 -> 4)
Output: 7 -> 8 -> 0 -> 7

题目要求：不能修改原始链表。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
    Stack<Integer> l1Stack = buildStack(l1);
    Stack<Integer> l2Stack = buildStack(l2);
    ListNode head = new ListNode(-1);
    int carry = 0;
    while (!l1Stack.isEmpty() || !l2Stack.isEmpty() || carry != 0) {
        int x = l1Stack.isEmpty() ? 0 : l1Stack.pop();
        int y = l2Stack.isEmpty() ? 0 : l2Stack.pop();
        int sum = x + y + carry;
        ListNode node = new ListNode(sum % 10);
        node.next = head.next;
        head.next = node;
        carry = sum / 10;
    }
    return head.next;
}

private Stack<Integer> buildStack(ListNode l) {
    Stack<Integer> stack = new Stack<>();
    while (l != null) {
        stack.push(l.val);
        l = l.next;
    }
    return stack;
}

8. 回文链表

234. Palindrome Linked List (Easy)

Leetcode / 力扣

题目要求：以 O(1) 的空间复杂度来求解。

切成两半，把后半段反转，然后比较两半是否相等。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public boolean isPalindrome(ListNode head) {
    if (head == null || head.next == null) return true;
    ListNode slow = head, fast = head.next;
    while (fast != null && fast.next != null) {
        slow = slow.next;
        fast = fast.next.next;
    }
    if (fast != null) slow = slow.next;  // 偶数节点，让 slow 指向下一个节点
    cut(head, slow);                     // 切成两个链表
    return isEqual(head, reverse(slow));
}

private void cut(ListNode head, ListNode cutNode) {
    while (head.next != cutNode) {
        head = head.next;
    }
    head.next = null;
}

private ListNode reverse(ListNode head) {
    ListNode newHead = null;
    while (head != null) {
        ListNode nextNode = head.next;
        head.next = newHead;
        newHead = head;
        head = nextNode;
    }
    return newHead;
}

private boolean isEqual(ListNode l1, ListNode l2) {
    while (l1 != null && l2 != null) {
        if (l1.val != l2.val) return false;
        l1 = l1.next;
        l2 = l2.next;
    }
    return true;
}

9. 分隔链表

725. Split Linked List in Parts(Medium)

Leetcode / 力扣

1
2
3
4
5
Input:
root = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10], k = 3
Output: [[1, 2, 3, 4], [5, 6, 7], [8, 9, 10]]
Explanation:
The input has been split into consecutive parts with size difference at most 1, and earlier parts are a larger size than the later parts.

题目描述：把链表分隔成 k 部分，每部分的长度都应该尽可能相同，排在前面的长度应该大于等于后面的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public ListNode[] splitListToParts(ListNode root, int k) {
    int N = 0;
    ListNode cur = root;
    while (cur != null) {
        N++;
        cur = cur.next;
    }
    int mod = N % k;
    int size = N / k;
    ListNode[] ret = new ListNode[k];
    cur = root;
    for (int i = 0; cur != null && i < k; i++) {
        ret[i] = cur;
        int curSize = size + (mod-- > 0 ? 1 : 0);
        for (int j = 0; j < curSize - 1; j++) {
            cur = cur.next;
        }
        ListNode next = cur.next;
        cur.next = null;
        cur = next;
    }
    return ret;
}

10. 链表元素按奇偶聚集

328. Odd Even Linked List (Medium)

Leetcode / 力扣

1
2
3
Example:
Given 1->2->3->4->5->NULL,
return 1->3->5->2->4->NULL.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public ListNode oddEvenList(ListNode head) {
    if (head == null) {
        return head;
    }
    ListNode odd = head, even = head.next, evenHead = even;
    while (even != null && even.next != null) {
        odd.next = odd.next.next;
        odd = odd.next;
        even.next = even.next.next;
        even = even.next;
    }
    odd.next = evenHead;
    return head;
}

展开全文 >>

分治

1. 给表达式加括号

241. Different Ways to Add Parentheses (Medium)

Leetcode / 力扣

1
2
3
4
5
6
Input: "2-1-1".

((2-1)-1) = 0
(2-(1-1)) = 2

Output : [0, 2]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public List<Integer> diffWaysToCompute(String input) {
    List<Integer> ways = new ArrayList<>();
    for (int i = 0; i < input.length(); i++) {
        char c = input.charAt(i);
        if (c == '+' || c == '-' || c == '*') {
            List<Integer> left = diffWaysToCompute(input.substring(0, i));
            List<Integer> right = diffWaysToCompute(input.substring(i + 1));
            for (int l : left) {
                for (int r : right) {
                    switch (c) {
                        case '+':
                            ways.add(l + r);
                            break;
                        case '-':
                            ways.add(l - r);
                            break;
                        case '*':
                            ways.add(l * r);
                            break;
                    }
                }
            }
        }
    }
    if (ways.size() == 0) {
        ways.add(Integer.valueOf(input));
    }
    return ways;
}

2. 不同的二叉搜索树

95. Unique Binary Search Trees II (Medium)

Leetcode / 力扣

给定一个数字 n，要求生成所有值为 1…n 的二叉搜索树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Input: 3
Output:
[
  [1,null,3,2],
  [3,2,null,1],
  [3,1,null,null,2],
  [2,1,3],
  [1,null,2,null,3]
]
Explanation:
The above output corresponds to the 5 unique BST's shown below:

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public List<TreeNode> generateTrees(int n) {
    if (n < 1) {
        return new LinkedList<TreeNode>();
    }
    return generateSubtrees(1, n);
}

private List<TreeNode> generateSubtrees(int s, int e) {
    List<TreeNode> res = new LinkedList<TreeNode>();
    if (s > e) {
        res.add(null);
        return res;
    }
    for (int i = s; i <= e; ++i) {
        List<TreeNode> leftSubtrees = generateSubtrees(s, i - 1);
        List<TreeNode> rightSubtrees = generateSubtrees(i + 1, e);
        for (TreeNode left : leftSubtrees) {
            for (TreeNode right : rightSubtrees) {
                TreeNode root = new TreeNode(i);
                root.left = left;
                root.right = right;
                res.add(root);
            }
        }
    }
    return res;
}

展开全文 >>

哈希表

哈希表使用 O(N) 空间复杂度存储数据，并且以 O(1) 时间复杂度求解问题。

  • Java 中的 HashSet 用于存储一个集合，可以查找元素是否在集合中。如果元素有穷，并且范围不大，那么可以用一个布尔数组来存储一个元素是否存在。例如对于只有小写字符的元素，就可以用一个长度为 26 的布尔数组来存储一个字符集合，使得空间复杂度降低为 O(1)。

    Java 中的 HashMap 主要用于映射关系，从而把两个元素联系起来。HashMap 也可以用来对元素进行计数统计，此时键为元素，值为计数。和 HashSet 类似，如果元素有穷并且范围不大，可以用整型数组来进行统计。在对一个内容进行压缩或者其它转换时，利用 HashMap 可以把原始内容和转换后的内容联系起来。例如在一个简化 url 的系统中 [Leetcdoe : 535. Encode and Decode TinyURL (Medium)

Leetcode，利用 HashMap 就可以存储精简后的 url 到原始 url 的映射，使得不仅可以显示简化的 url，也可以根据简化的 url 得到原始 url 从而定位到正确的资源�) / 力扣，利用 HashMap 就可以存储精简后的 url 到原始 url 的映射，使得不仅可以显示简化的 url，也可以根据简化的 url 得到原始 url 从而定位到正确的资源�)

1. 数组中两个数的和为给定值

1. Two Sum (Easy)

Leetcode / 力扣

可以先对数组进行排序，然后使用双指针方法或者二分查找方法。这样做的时间复杂度为 O(NlogN)，空间复杂度为 O(1)。

用 HashMap 存储数组元素和索引的映射，在访问到 nums[i] 时，判断 HashMap 中是否存在 target - nums[i]，如果存在说明 target - nums[i] 所在的索引和 i 就是要找的两个数。该方法的时间复杂度为 O(N)，空间复杂度为 O(N)，使用空间来换取时间。

1
2
3
4
5
6
7
8
9
10
11
public int[] twoSum(int[] nums, int target) {
    HashMap<Integer, Integer> indexForNum = new HashMap<>();
    for (int i = 0; i < nums.length; i++) {
        if (indexForNum.containsKey(target - nums[i])) {
            return new int[]{indexForNum.get(target - nums[i]), i};
        } else {
            indexForNum.put(nums[i], i);
        }
    }
    return null;
}

2. 判断数组是否含有重复元素

217. Contains Duplicate (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
public boolean containsDuplicate(int[] nums) {
    Set<Integer> set = new HashSet<>();
    for (int num : nums) {
        set.add(num);
    }
    return set.size() < nums.length;
}

3. 最长和谐序列

594. Longest Harmonious Subsequence (Easy)

Leetcode / 力扣

1
2
3
Input: [1,3,2,2,5,2,3,7]
Output: 5
Explanation: The longest harmonious subsequence is [3,2,2,2,3].

和谐序列中最大数和最小数之差正好为 1，应该注意的是序列的元素不一定是数组的连续元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
public int findLHS(int[] nums) {
    Map<Integer, Integer> countForNum = new HashMap<>();
    for (int num : nums) {
        countForNum.put(num, countForNum.getOrDefault(num, 0) + 1);
    }
    int longest = 0;
    for (int num : countForNum.keySet()) {
        if (countForNum.containsKey(num + 1)) {
            longest = Math.max(longest, countForNum.get(num + 1) + countForNum.get(num));
        }
    }
    return longest;
}

4. 最长连续序列

128. Longest Consecutive Sequence (Hard)

Leetcode / 力扣

1
2
Given [100, 4, 200, 1, 3, 2],
The longest consecutive elements sequence is [1, 2, 3, 4]. Return its length: 4.

要求以 O(N) 的时间复杂度求解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public int longestConsecutive(int[] nums) {
    Map<Integer, Integer> countForNum = new HashMap<>();
    for (int num : nums) {
        countForNum.put(num, 1);
    }
    for (int num : nums) {
        forward(countForNum, num);
    }
    return maxCount(countForNum);
}

private int forward(Map<Integer, Integer> countForNum, int num) {
    if (!countForNum.containsKey(num)) {
        return 0;
    }
    int cnt = countForNum.get(num);
    if (cnt > 1) {
        return cnt;
    }
    cnt = forward(countForNum, num + 1) + 1;
    countForNum.put(num, cnt);
    return cnt;
}

private int maxCount(Map<Integer, Integer> countForNum) {
    int max = 0;
    for (int num : countForNum.keySet()) {
        max = Math.max(max, countForNum.get(num));
    }
    return max;
}

展开全文 >>

二分查找

正常实现 

1
2
3
Input : [1,2,3,4,5]
key : 3
return the index : 2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
public int binarySearch(int[] nums, int key) {
    int l = 0, h = nums.length - 1;
    while (l <= h) {
        int m = l + (h - l) / 2;
        if (nums[m] == key) {
            return m;
        } else if (nums[m] > key) {
            h = m - 1;
        } else {
            l = m + 1;
        }
    }
    return -1;
}

时间复杂度

二分查找也称为折半查找，每次都能将查找区间减半，这种折半特性的算法时间复杂度为 O(logN)。

m 计算

有两种计算中值 m 的方式：

  • m = (l + h) / 2
  • m = l + (h - l) / 2

l + h 可能出现加法溢出，也就是说加法的结果大于整型能够表示的范围。但是 l 和 h 都为正数，因此 h - l 不会出现加法溢出问题。所以，最好使用第二种计算法方法。

未成功查找的返回值

循环退出时如果仍然没有查找到 key，那么表示查找失败。可以有两种返回值：

  • -1：以一个错误码表示没有查找到 key
  • l：将 key 插入到 nums 中的正确位置

变种

二分查找可以有很多变种，实现变种要注意边界值的判断。例如在一个有重复元素的数组中查找 key 的最左位置的实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
public int binarySearch(int[] nums, int key) {
    int l = 0, h = nums.length;
    while (l < h) {
        int m = l + (h - l) / 2;
        if (nums[m] >= key) {
            h = m;
        } else {
            l = m + 1;
        }
    }
    return l;
}

该实现和正常实现有以下不同：

  • h 的赋值表达式为 h = m
  • 循环条件为 l < h
  • 最后返回 l 而不是 -1

在 nums[m] >= key 的情况下，可以推导出最左 key 位于 [l, m] 区间中，这是一个闭区间。h 的赋值表达式为 h = m，因为 m 位置也可能是解。

在 h 的赋值表达式为 h = m 的情况下，如果循环条件为 l <= h，那么会出现循环无法退出的情况，因此循环条件只能是 l < h。以下演示了循环条件为 l <= h 时循环无法退出的情况：

1
2
3
4
5
6
7
nums = {0, 1, 2}, key = 1
l   m   h
0   1   2  nums[m] >= key
0   0   1  nums[m] < key
1   1   1  nums[m] >= key
1   1   1  nums[m] >= key
...

当循环体退出时，不表示没有查找到 key，因此最后返回的结果不应该为 -1。为了验证有没有查找到，需要在调用端判断一下返回位置上的值和 key 是否相等。

1. 求开方

69. Sqrt(x) (Easy)

Leetcode / 力扣

1
2
3
4
5
6
Input: 4
Output: 2

Input: 8
Output: 2
Explanation: The square root of 8 is 2.82842..., and since we want to return an integer, the decimal part will be truncated.

一个数 x 的开方 sqrt 一定在 0 ~ x 之间，并且满足 sqrt == x / sqrt。可以利用二分查找在 0 ~ x 之间查找 sqrt。

对于 x = 8，它的开方是 2.82842…，最后应该返回 2 而不是 3。在循环条件为 l <= h 并且循环退出时，h 总是比 l 小 1，也就是说 h = 2，l = 3，因此最后的返回值应该为 h 而不是 l。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public int mySqrt(int x) {
    if (x <= 1) {
        return x;
    }
    int l = 1, h = x;
    while (l <= h) {
        int mid = l + (h - l) / 2;
        int sqrt = x / mid;
        if (sqrt == mid) {
            return mid;
        } else if (mid > sqrt) {
            h = mid - 1;
        } else {
            l = mid + 1;
        }
    }
    return h;
}

2. 大于给定元素的最小元素

744. Find Smallest Letter Greater Than Target (Easy)

Leetcode / 力扣

1
2
3
4
5
6
7
8
9
Input:
letters = ["c", "f", "j"]
target = "d"
Output: "f"

Input:
letters = ["c", "f", "j"]
target = "k"
Output: "c"

题目描述：给定一个有序的字符数组 letters 和一个字符 target，要求找出 letters 中大于 target 的最小字符，如果找不到就返回第 1 个字符。

1
2
3
4
5
6
7
8
9
10
11
12
13
public char nextGreatestLetter(char[] letters, char target) {
    int n = letters.length;
    int l = 0, h = n - 1;
    while (l <= h) {
        int m = l + (h - l) / 2;
        if (letters[m] <= target) {
            l = m + 1;
        } else {
            h = m - 1;
        }
    }
    return l < n ? letters[l] : letters[0];
}

3. 有序数组的 Single Element

540. Single Element in a Sorted Array (Medium)

Leetcode / 力扣

1
2
Input: [1, 1, 2, 3, 3, 4, 4, 8, 8]
Output: 2

题目描述：一个有序数组只有一个数不出现两次，找出这个数。

要求以 O(logN) 时间复杂度进行求解，因此不能遍历数组并进行异或操作来求解，这么做的时间复杂度为 O(N)。

令 index 为 Single Element 在数组中的位置。在 index 之后，数组中原来存在的成对状态被改变。如果 m 为偶数，并且 m + 1 < index，那么 nums[m] == nums[m + 1]；m + 1 >= index，那么 nums[m] != nums[m + 1]。

从上面的规律可以知道，如果 nums[m] == nums[m + 1]，那么 index 所在的数组位置为 [m + 2, h]，此时令 l = m + 2；如果 nums[m] != nums[m + 1]，那么 index 所在的数组位置为 [l, m]，此时令 h = m。

因为 h 的赋值表达式为 h = m，那么循环条件也就只能使用 l < h 这种形式。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int singleNonDuplicate(int[] nums) {
    int l = 0, h = nums.length - 1;
    while (l < h) {
        int m = l + (h - l) / 2;
        if (m % 2 == 1) {
            m--;   // 保证 l/h/m 都在偶数位，使得查找区间大小一直都是奇数
        }
        if (nums[m] == nums[m + 1]) {
            l = m + 2;
        } else {
            h = m;
        }
    }
    return nums[l];
}

4. 第一个错误的版本

278. First Bad Version (Easy)

Leetcode / 力扣

题目描述：给定一个元素 n 代表有 [1, 2, …, n] 版本，在第 x 位置开始出现错误版本，导致后面的版本都错误。可以调用 isBadVersion(int x) 知道某个版本是否错误，要求找到第一个错误的版本。

如果第 m 个版本出错，则表示第一个错误的版本在 [l, m] 之间，令 h = m；否则第一个错误的版本在 [m + 1, h] 之间，令 l = m + 1。

因为 h 的赋值表达式为 h = m，因此循环条件为 l < h。

1
2
3
4
5
6
7
8
9
10
11
12
public int firstBadVersion(int n) {
    int l = 1, h = n;
    while (l < h) {
        int mid = l + (h - l) / 2;
        if (isBadVersion(mid)) {
            h = mid;
        } else {
            l = mid + 1;
        }
    }
    return l;
}

5. 旋转数组的最小数字

153. Find Minimum in Rotated Sorted Array (Medium)

Leetcode / 力扣

1
2
Input: [3,4,5,1,2],
Output: 1
1
2
3
4
5
6
7
8
9
10
11
12
public int findMin(int[] nums) {
    int l = 0, h = nums.length - 1;
    while (l < h) {
        int m = l + (h - l) / 2;
        if (nums[m] <= nums[h]) {
            h = m;
        } else {
            l = m + 1;
        }
    }
    return nums[l];
}

6. 查找区间

34. Find First and Last Position of Element in Sorted Array

Leetcode / 力扣

1
2
3
4
5
Input: nums = [5,7,7,8,8,10], target = 8
Output: [3,4]

Input: nums = [5,7,7,8,8,10], target = 6
Output: [-1,-1]

题目描述：给定一个有序数组 nums 和一个目标 target，要求找到 target 在 nums 中的第一个位置和最后一个位置。

可以用二分查找找出第一个位置和最后一个位置，但是寻找的方法有所不同，需要实现两个二分查找。我们将寻找 target 最后一个位置，转换成寻找 target+1 第一个位置，再往前移动一个位置。这样我们只需要实现一个二分查找代码即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public int[] searchRange(int[] nums, int target) {
    int first = findFirst(nums, target);
    int last = findFirst(nums, target + 1) - 1;
    if (first == nums.length || nums[first] != target) {
        return new int[]{-1, -1};
    } else {
        return new int[]{first, Math.max(first, last)};
    }
}

private int findFirst(int[] nums, int target) {
    int l = 0, h = nums.length; // 注意 h 的初始值
    while (l < h) {
        int m = l + (h - l) / 2;
        if (nums[m] >= target) {
            h = m;
        } else {
            l = m + 1;
        }
    }
    return l;
}

在寻找第一个位置的二分查找代码中，需要注意 h 的取值为 nums.length，而不是 nums.length - 1。先看以下示例：

1
nums = [2,2], target = 2

如果 h 的取值为 nums.length - 1，那么 last = findFirst(nums, target + 1) - 1 = 1 - 1 = 0。这是因为 findLeft 只会返回 [0, nums.length - 1] 范围的值，对于 findFirst([2,2], 3) ，我们希望返回 3 插入 nums 中的位置，也就是数组最后一个位置再往后一个位置，即 nums.length。所以我们需要将 h 取值为 nums.length，从而使得 findFirst返回的区间更大，能够覆盖 target 大于 nums 最后一个元素的情况。

展开全文 >>

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia-plus根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

LHS

面朝大海
春暖花开